Visualizing a Map of Walter Christaller, Poland 1941
Part I:  Benchmarking the Map

Sandra Lach Arlinghaus

Adjunct Professor of Mathematical Geography and Population-Environment Dynamics
School of Natural Resources and Environment, The University of Michigan, Ann Arbor

Please set screen to highest resolution and use a high speed internet connection.
Please download the most recent free version of Google Earth®.  Make sure the "Terrain" box in Google Earth® is checked.

Links to files to download for use in Google Earth®

Bringing an Historical Map Across the Digital Divide

One complex system from the early 20th century in the history of geography is the development, by Walter Christaller, of a theory of settlement locations:  central place theory.  The communication of his ideas is in the printed format of the times.  There are black and white maps of complex systems of pattern; they tell one story.  What might they look like, however, when recast using contemporary capability?  How might this capability expand the research frontier?    The sequence of images and text below will examine a single map of Christaller, from a 1941 document, and bring it into the virtual reality of Google Earth®.  When the reader downloads the files above, the power of the Internet is harnessed to permit him/her to replicate the results of the article while reading it and to experiment with related ideas at the same time.  Such capability is an important aspect of scientific communication.

Settlements in Eastern Europe:  Walter Christaller

Figure 1 shows Christaller's 1941 map of a proposed settlement pattern in Eastern Europe (in the western and central parts of what is today, Poland).  Cities, towns, or villages are marked with circles of varying size where the size of the circle represents the number of inhabitants proposed to make up the population.  The largest circles represent cities of 450,000 inhabitants, the next largest 100,000, the third largest 30,000 and so on according to the legend.  The regional boundaries of varying line weight are drawn also to include a fixed number of inhabitants:  the largest region is to include 2.7 million inhabitants, the next largest 210,000 inhabitants, and so on according to the legend.  The map from 1941 is a remarkable cartographic effort:  layer upon layer is meticulously drawn and labelled by hand.  One might speculate in various ways about adjacency patterns, spacing patterns, or others on the existing map.  Understanding such patterns from maps is often aided by having the full picture on the map:  terrain, physical features, three dimensional effects, and so forth.  The map that Christaller drew is already complicated; introducing physical or other features would clutter this two dimensional map and destroy its legibility. 


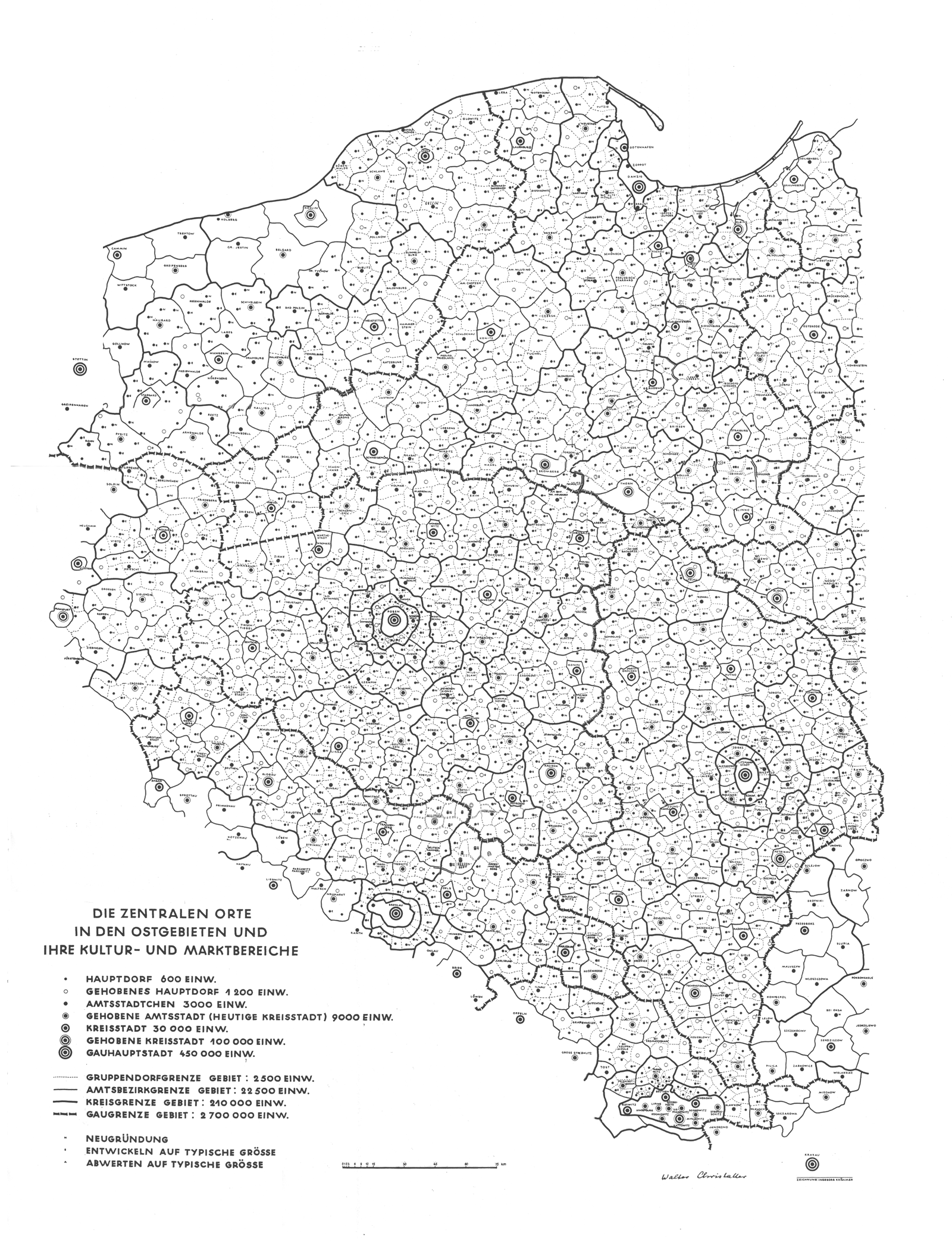Figure 1.  Christaller's map of proposed settlement patterns in Eastern Europe, 1941.  Both city/town and regional values are determined by prescribed number of inhabitants to occupy the city or region.  [See reference at end].

Figure 2 shows the map from Figure 1 brought directly into Google Earth® where one sees immediately the possibility of visualizing the map in relation to the terrain.  When the opaque map is placed on the surface, it is difficult to align the map with the globe.  Activating the "populated places" checkbox in Google Earth® brings up a set of points to use as established positions to see if the alignment of the paper map with the software is reasonable.   For additional context in the virtual environment of Google Earth® current subnational boundary files are introduced [see reference to Valery35 and Barmigan for link].  The paper map is made semi-transparent to see simultaneously both the original map and the globe under it.  The paper map is manipulated in various ways, suggested in the animation sequence, to improve the alignment.  Despite considerable maneuvering, the paper map does not line up very well with the Google Earth® image.  Bydgoszcz on the globe should line up with Bromberg on the map; Torun on the globe should line up with Thorn on the map; Lodz on the globe should line up with Litzmannstadt on the map; Poznan on the globe should line up with Posen on the map; Wroclaw on the globe should line up with Breslau on the map; and so forth.   The needed alignment is not present and cannot be made to work simply by importing the map and adjusting its position in relation to known positions.  The reader wishing to try may do so using basemaps contained in the second downloaded file from the top of this article.


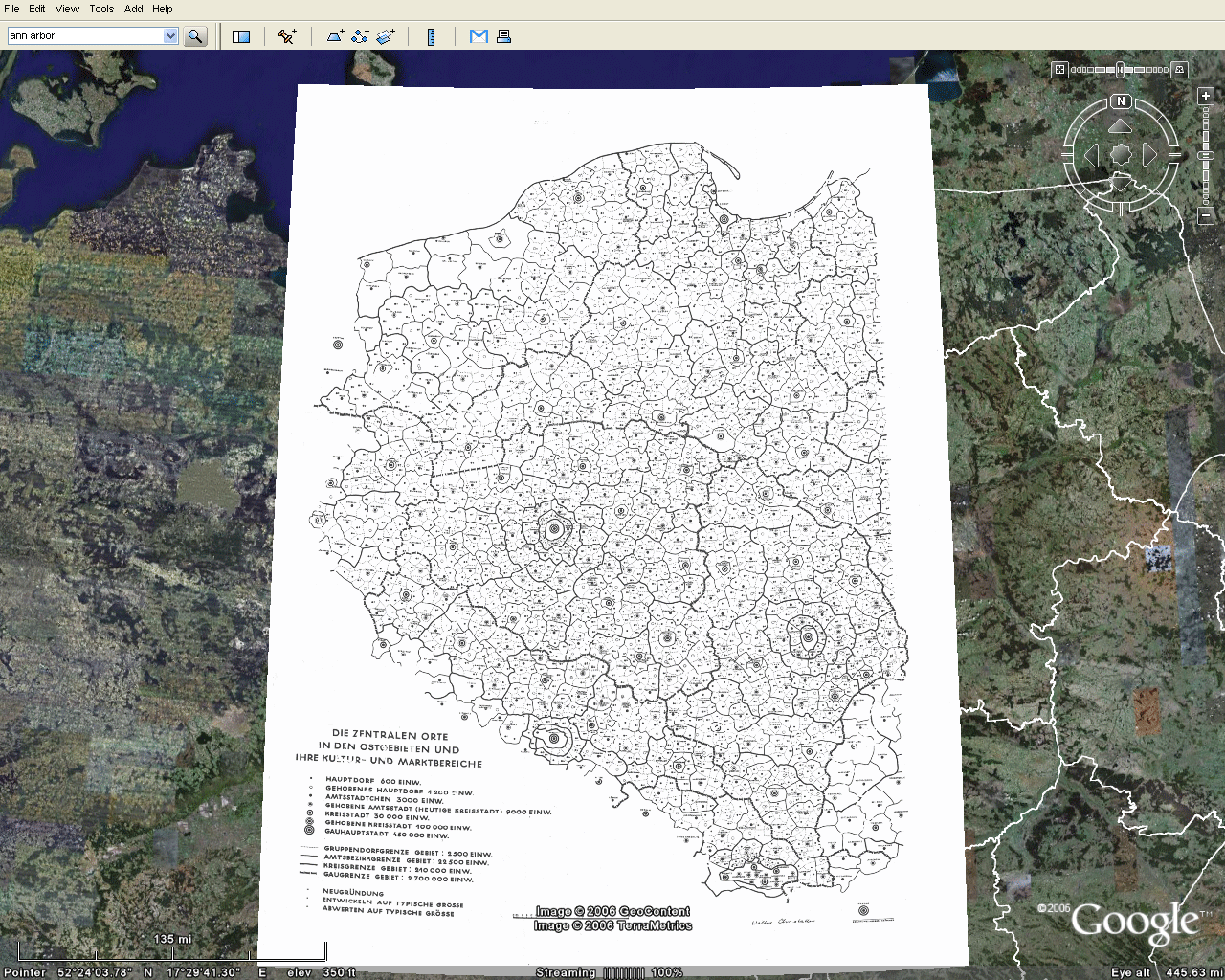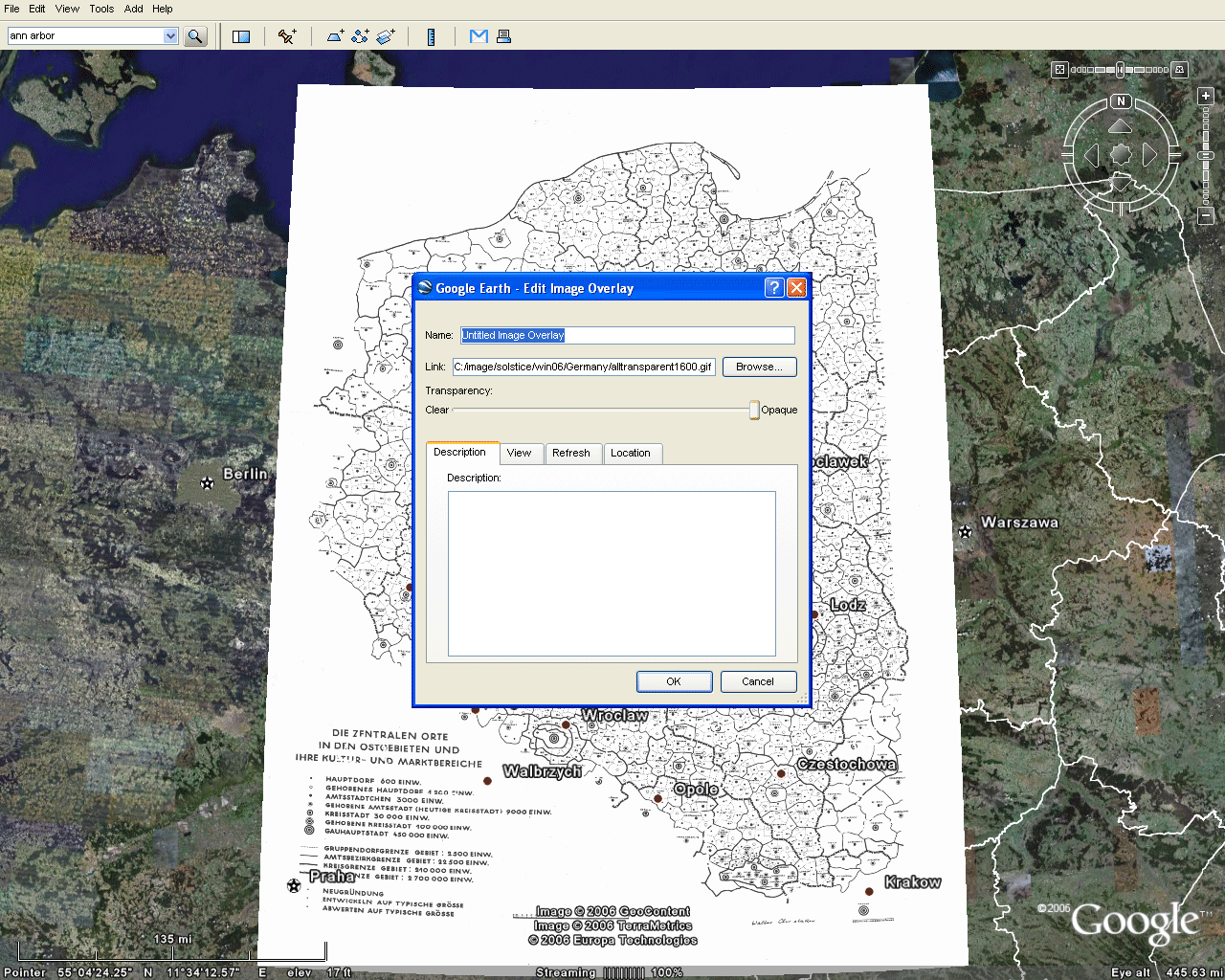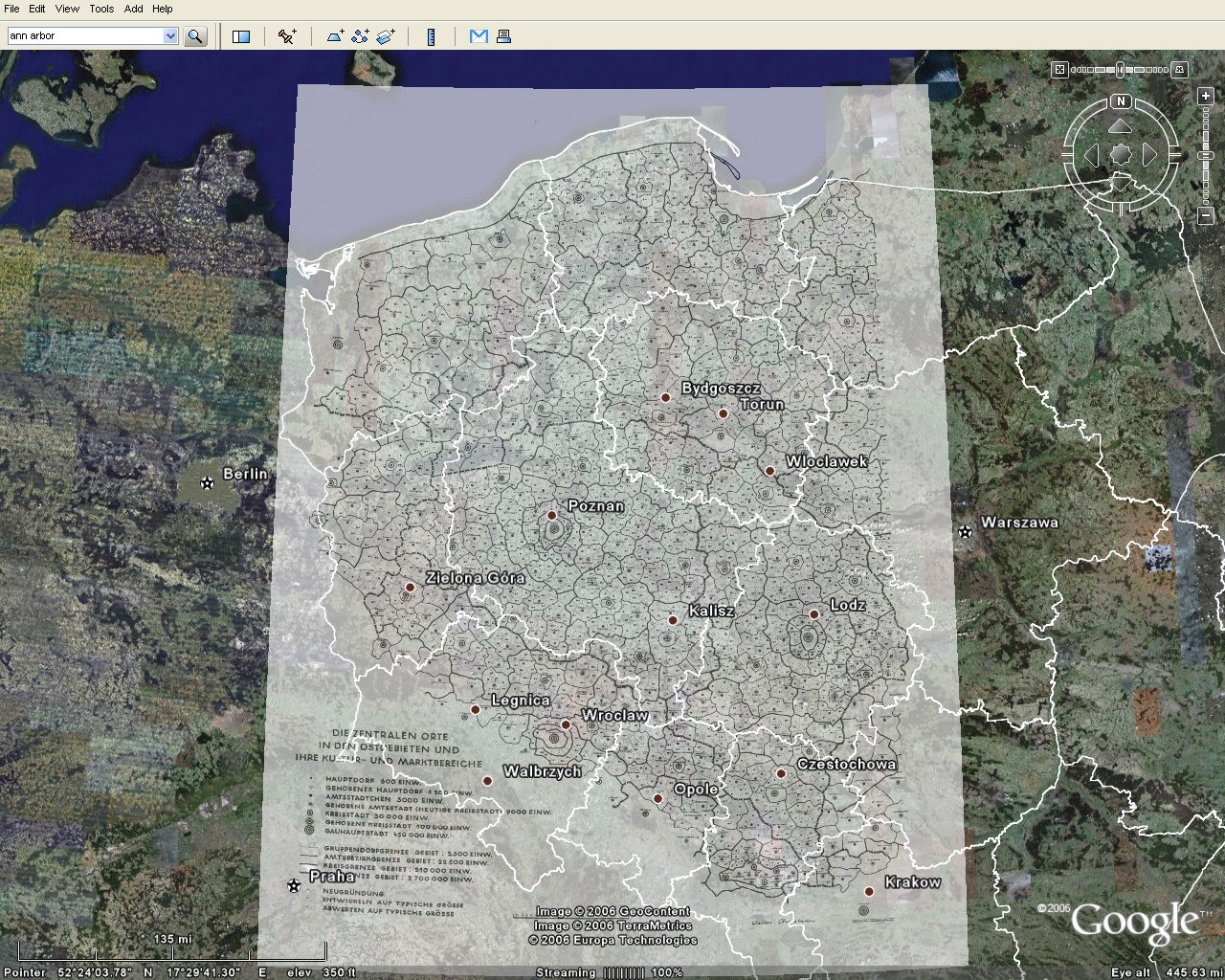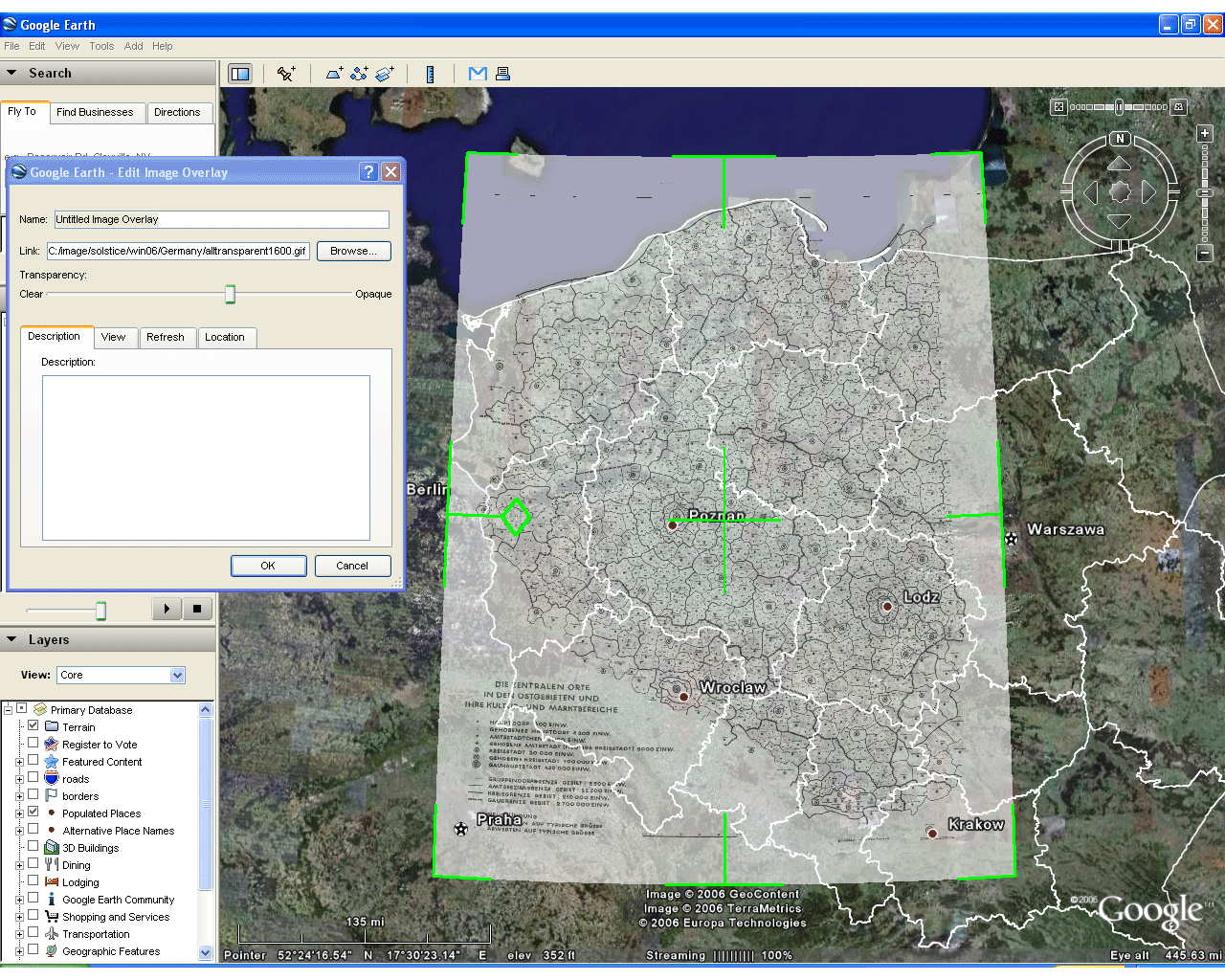Figure 2

Aligning the Paper Map on the Virtual Earth

Benchmarks

The set of cities already present in Google Earth® was used in Figure 2 as a set of known positions against which to test imported map position.  There are two sets of locations: 
Choose from the intersection of these two sets, all Christaller cities and towns in the three largest categories.  Find their corresponding positions on the Google Earth® globe.  All of those Christaller cities and towns do appear in the Google Earth® set although one may need to do a bit of research on place names to translate the 1941 place names to the corresponding 2006 place names.   Benchmarks are carefully positioned reference points from which to infer, or interpolate, other positions.  The set of locations just identified in Google Earth®, as the virtual locations corresponding to the top three point categories in the Christaller hierarchy, will serve as a set of benchmarks in the virtual world against which to test position in that world.  The image in Figure 3 shows these benchmarks portrayed as rods planted on the globe with rod height corresponding to Christaller hierarchical rank:
The rods emphasize benchmark position.  They are translucent so one can see the terrain through them.  Structures such as this are easy to create in either Google SketchUp® (free software) that can then be imported to Google Earth® (free software) [see Appendix to Part I of article by Arlinghaus and Batty in this journal].  Or, they can be created directly in Google Earth Pro® (not free)

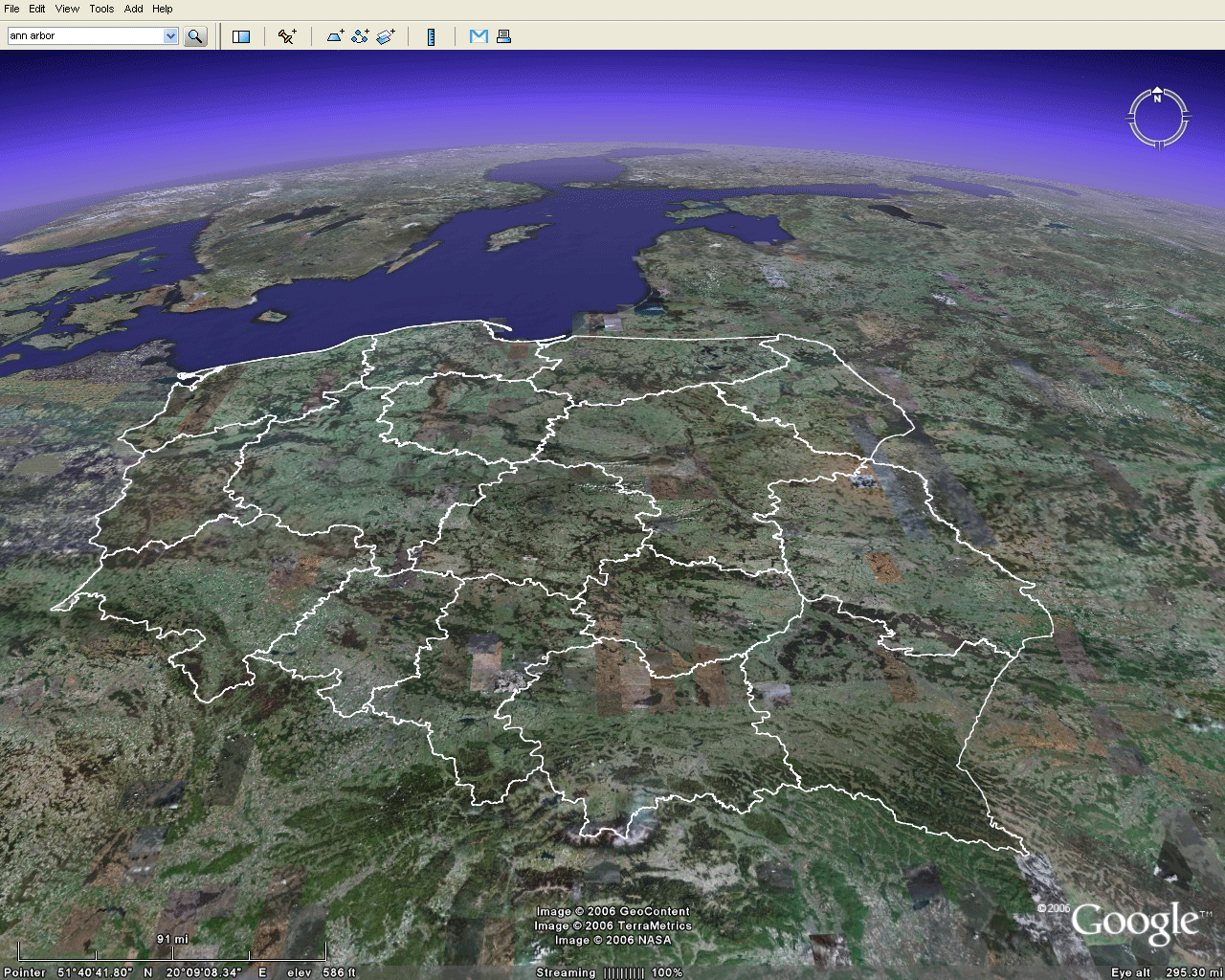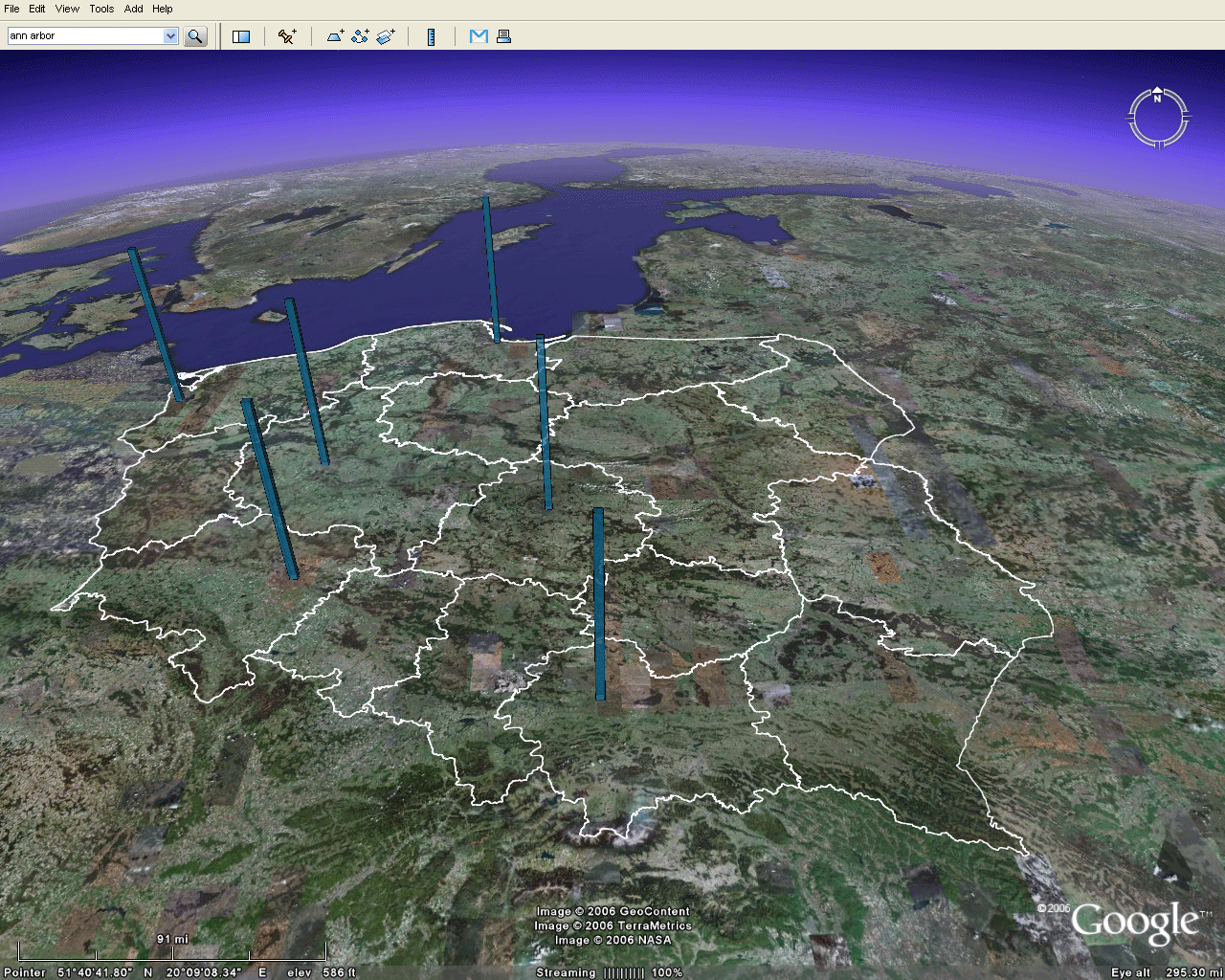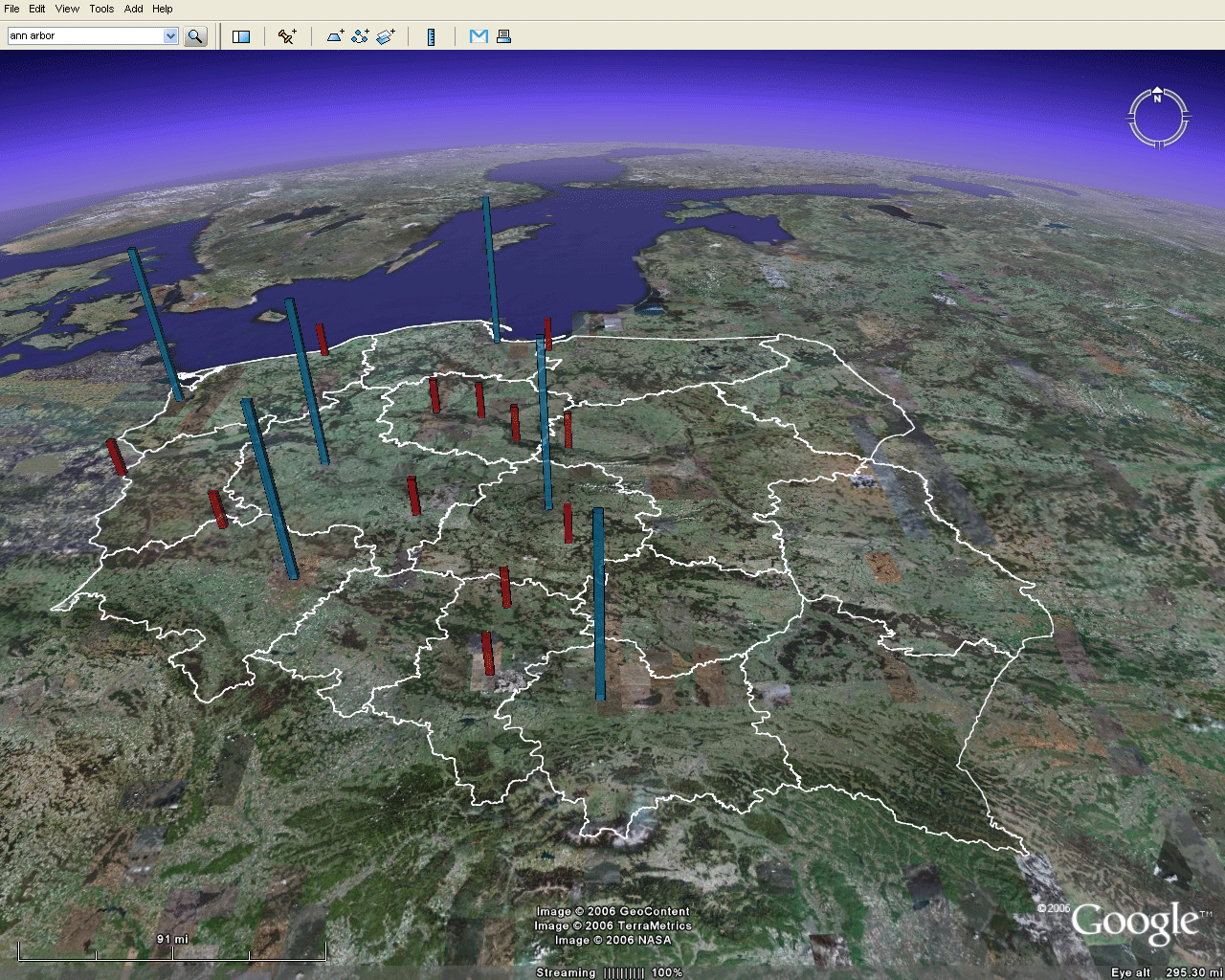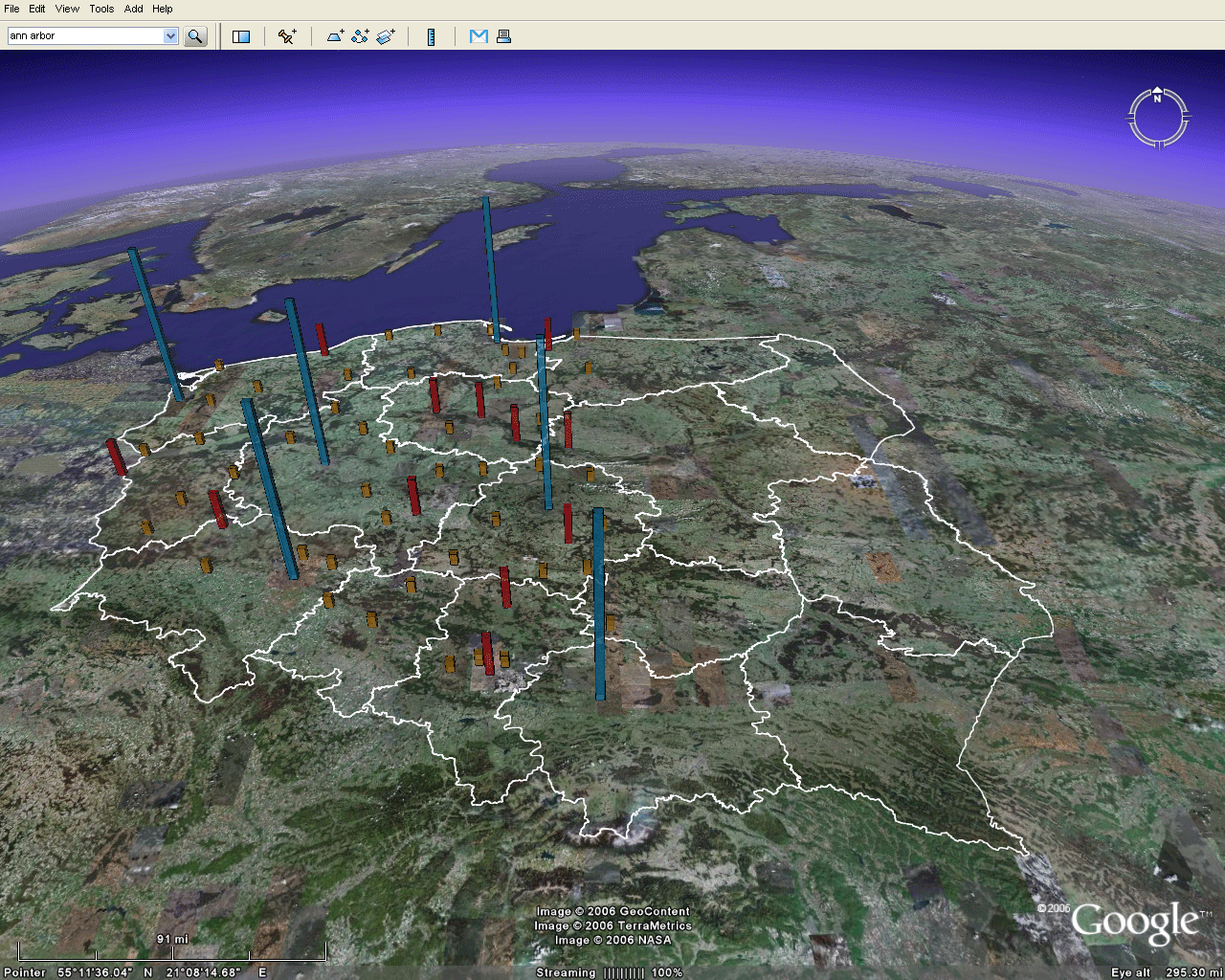Figure 3.  Benchmarks.  The blue rods represent locations for cities in the top Christaller category; the red one in the second; and, the gold ones in the third.


Use of the benchmarks for map alignment

The maps in Figure 3 show the position of a subset of Christaller points as benchmarks for extracting the rest of the information from the map.  The remaining images in this section suggest ways to use these benchmarks to improve the fit of the map with the surface of the virtual Earth.  Figure 4 illustrates the location of the flat map with respect to the benchmarks:  clearly, the benchmarks in the virtual world cannot be made to line up with the existing map.  One way to improve the fit may be to disassemble the Christaller map into smaller regions, fit thesmaller regions to the benchmarks, and then reassemble the information.

Smaller regions assigned to benchmarks produce a better fit of benchmarks to the map.  Such an assignment strategy also spreads the error across the map, away from the benchmarks.  Thus, while there are no particular standards for accuracy associated with this sort of mapping in the virtual world, the same ideas apply as when mapping the physical world.  Figure out where the error is and tell the reader about it.  If possible, develop a quantitative measure to ensure replicable communication (often, when using control points to digitize a map in Geographic Information Systems software, one finds a Root Mean Square error of 0.004 as a default setting). 


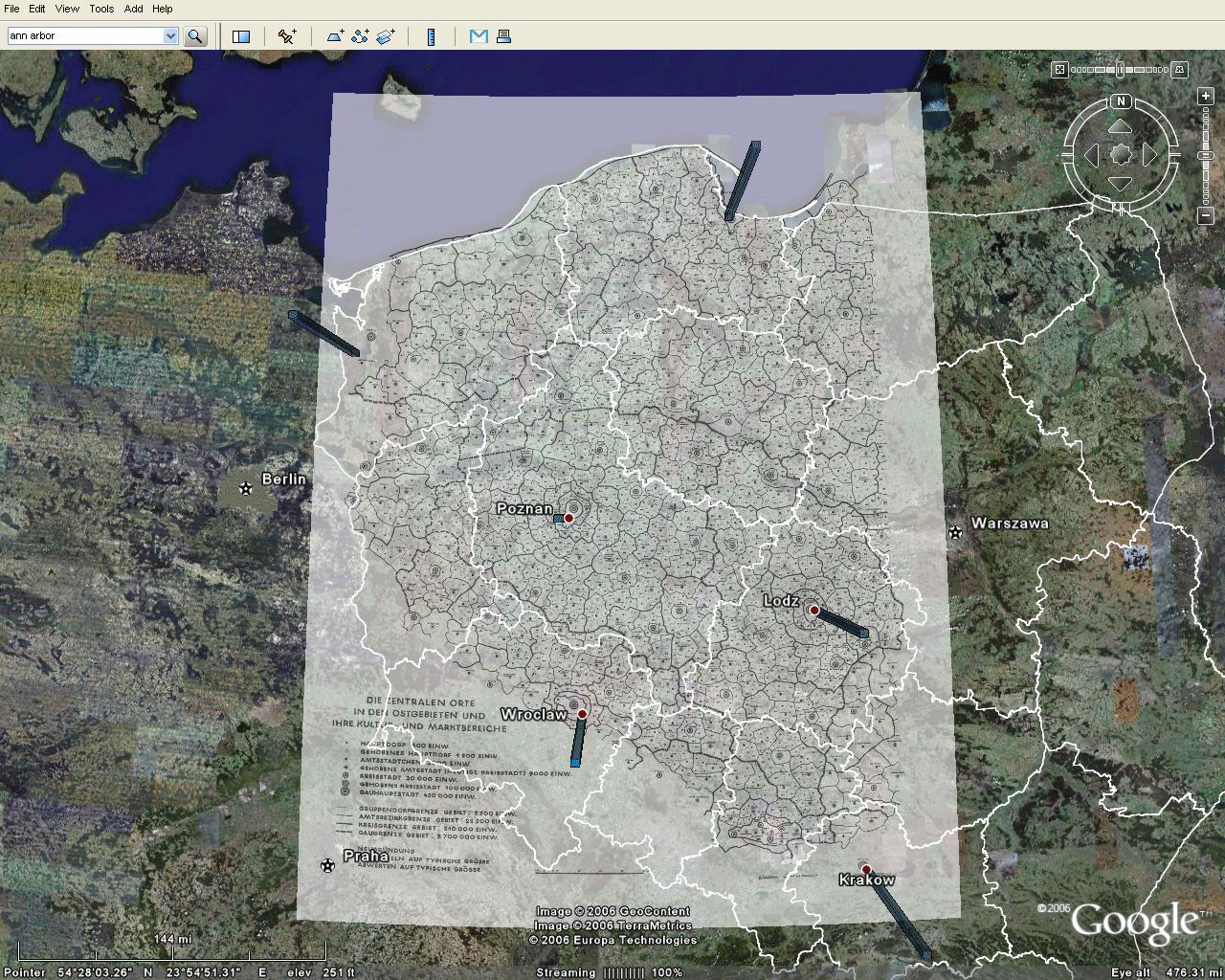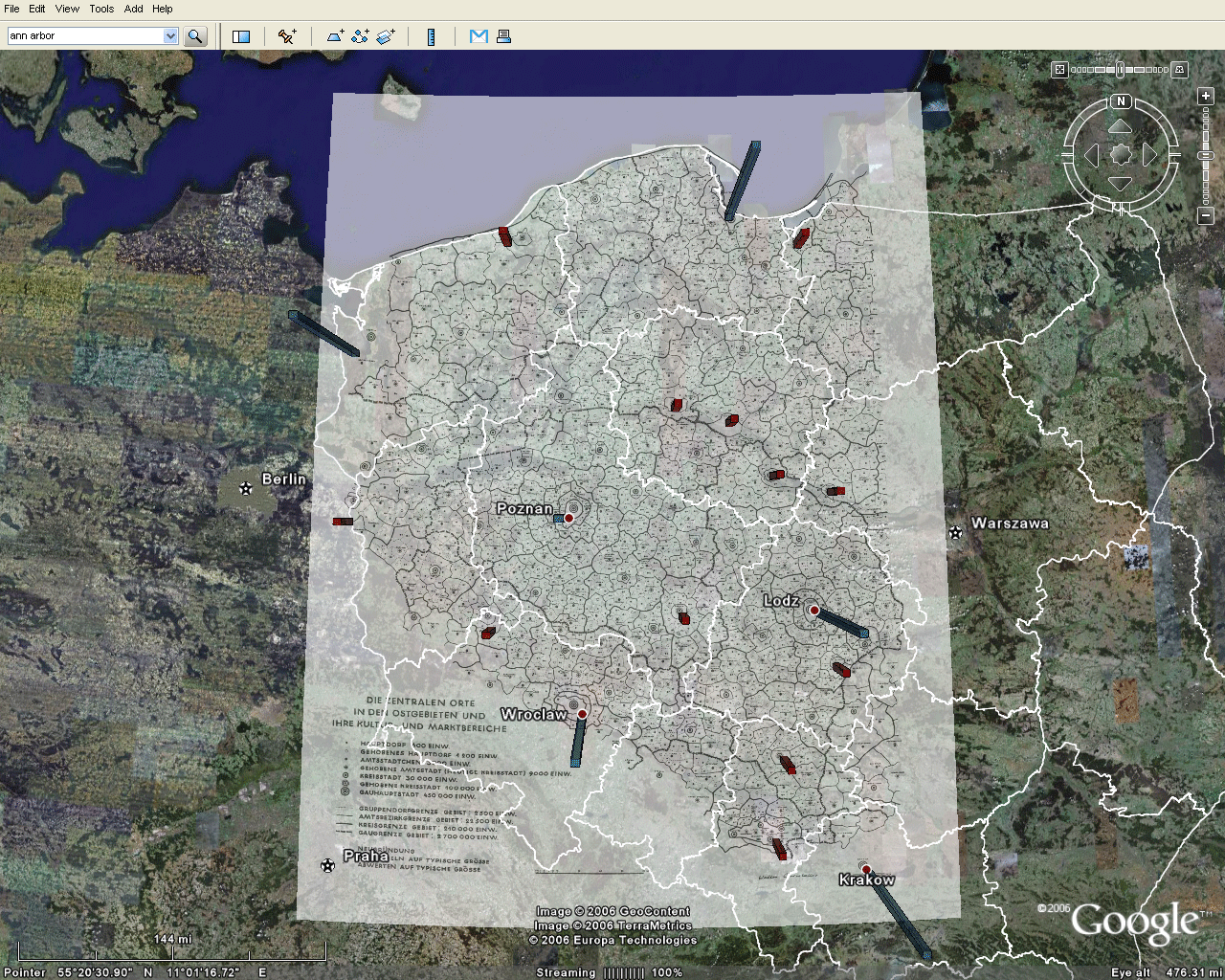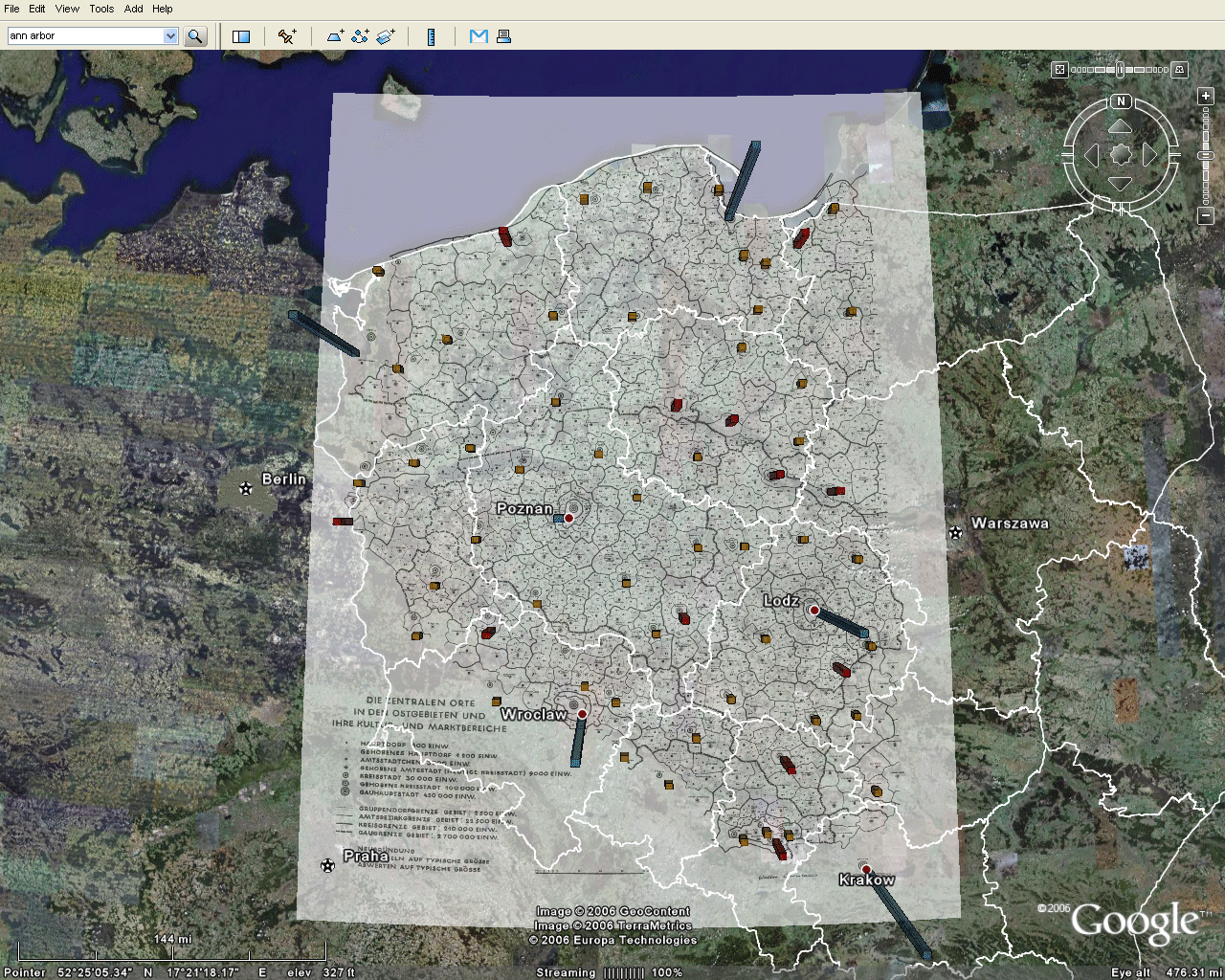Figure 4


Map Disassembly:  Use of the Christaller 2.7  million regions

The Christaller hierarchy associated with place size was used to create a set of mapping benchmarks.  It is natural, then, to use the regions in the Christaller hierarchy as the regions in which to disassemble the map.  The largest regions in the Christaller map are those designed for 2.7 million inhabitants.  Will these regions be small enough?  Figure 5 shows the results of using the three largest 2.7 million regions:  only the full regions within the map (with Danzig, Litzmannstadt, and Posen as largest cities).  The fit of benchmarks in the virtual world to this set of smaller maps is better than it is using the entire map.  Nonetheless, there is still much room for improvement.  The blue rods necessarily fit, as the foci of the 2.7 million regions, but many of the red rods and gold rods clearly miss the mark.  The reader wishing to experiment with alignment may do so, as well.  These files are contained in the files at the top of this article.

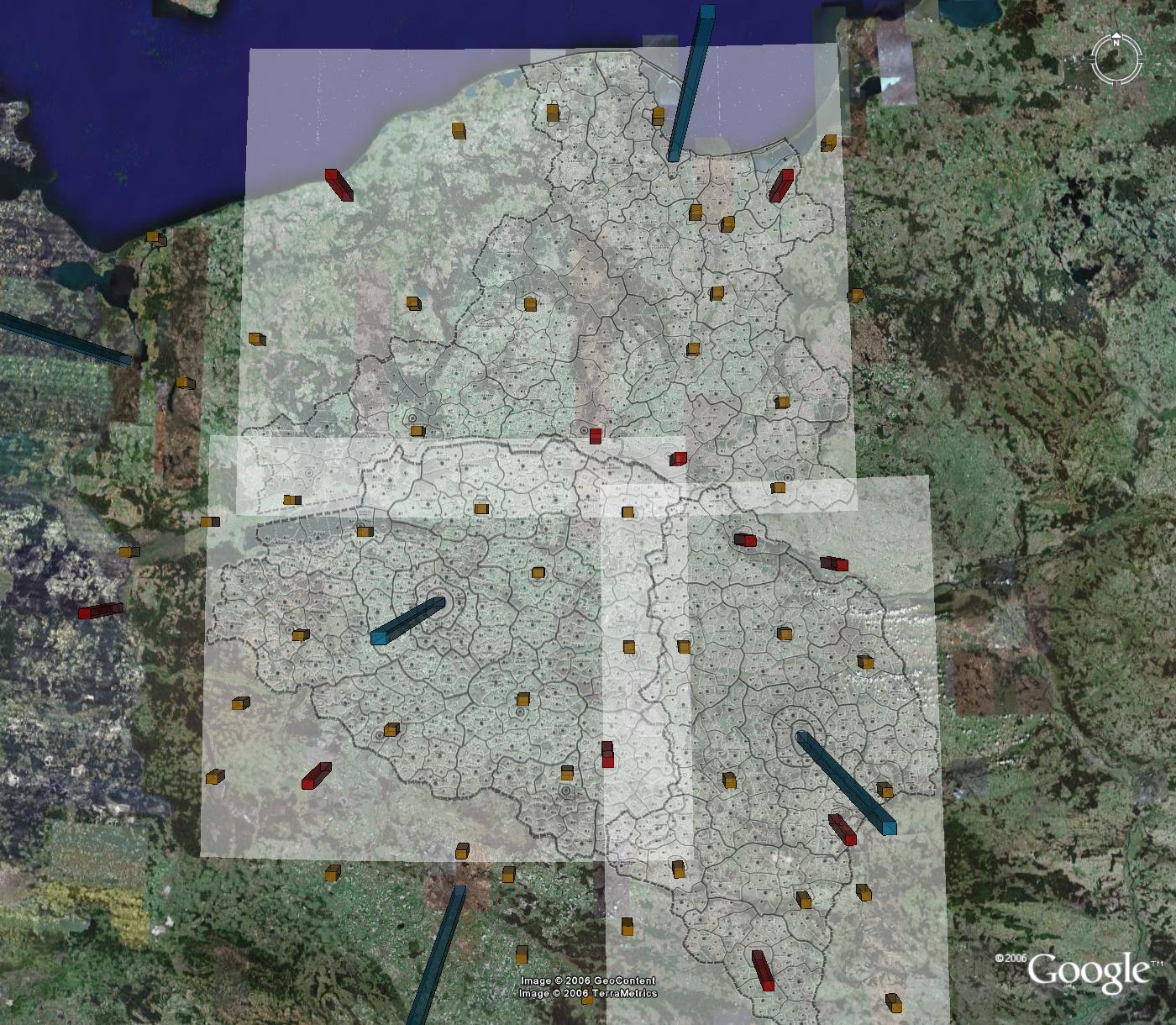Figure 5.  Alignment of Christaller map with underlying Earth image.  The blue rods necessarily fit, as the foci of the 2.7 million regions,  but many of the red and gold rods clearly miss the mark.


Map Disassembly:  Use of the Christaller 210,000 regions

Assigning transparency in Google Earth® is helpful in seeing, simultaneously, both the map and what is under the map.  Another approach that is also useful, especially when looking at detail, is first to remove the polygon interiors from the map.  This procedure is simple to execute:  save the map pieces in .gif format and assign transparency to white colors.  Figure 6 shows an animated sequence of Christaller 2.7 million full regions (Danzig, Litzmannstadt, and Posen) disassembled into the smaller Christaller 210,000 regions and saved as transparent .gifs.  (One advance-reader noted the peculiarity that Danzig, as a highest order central place,  is not in the center of its apparently "complete" region.)



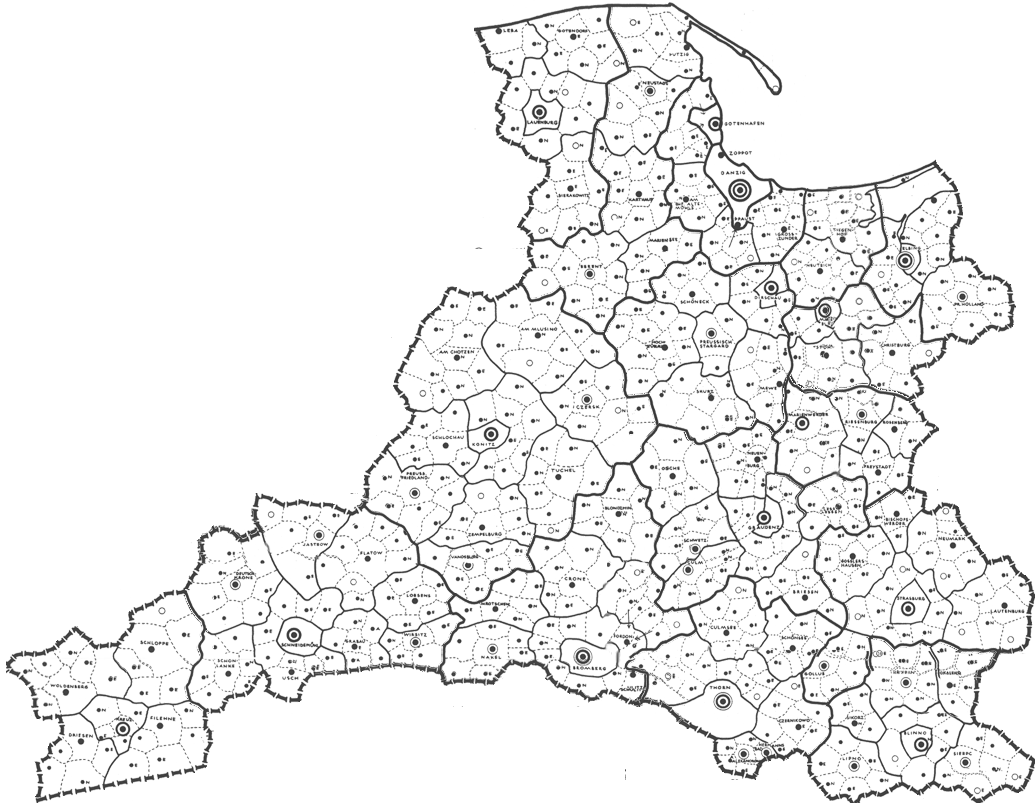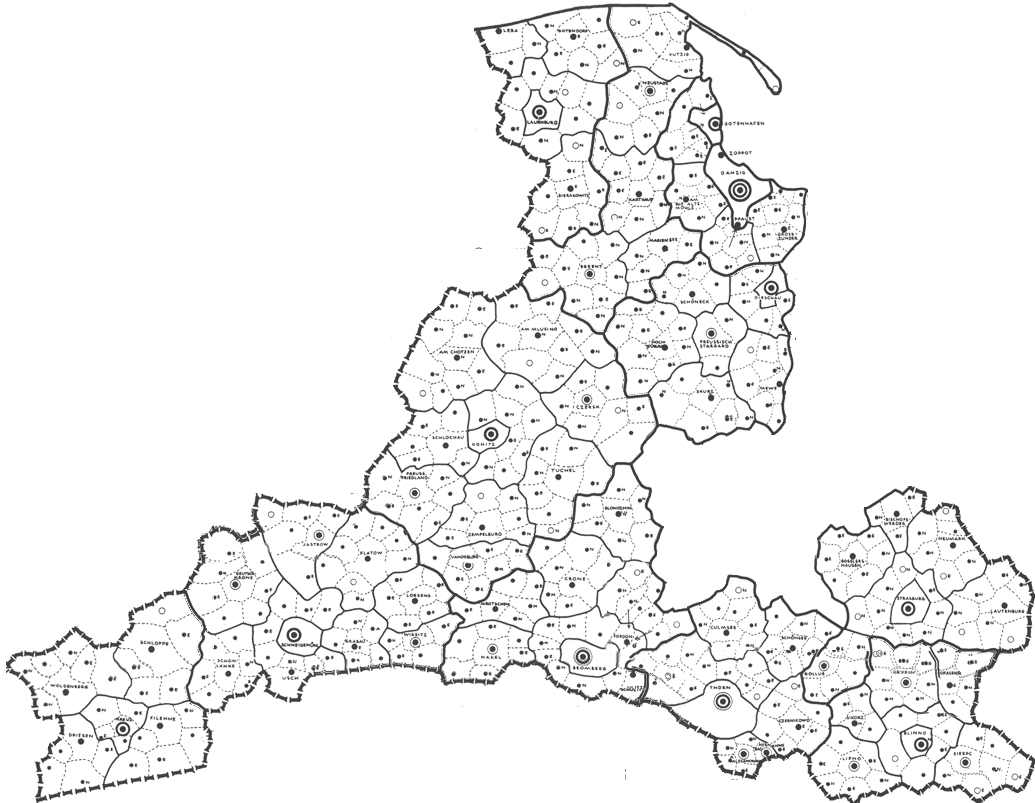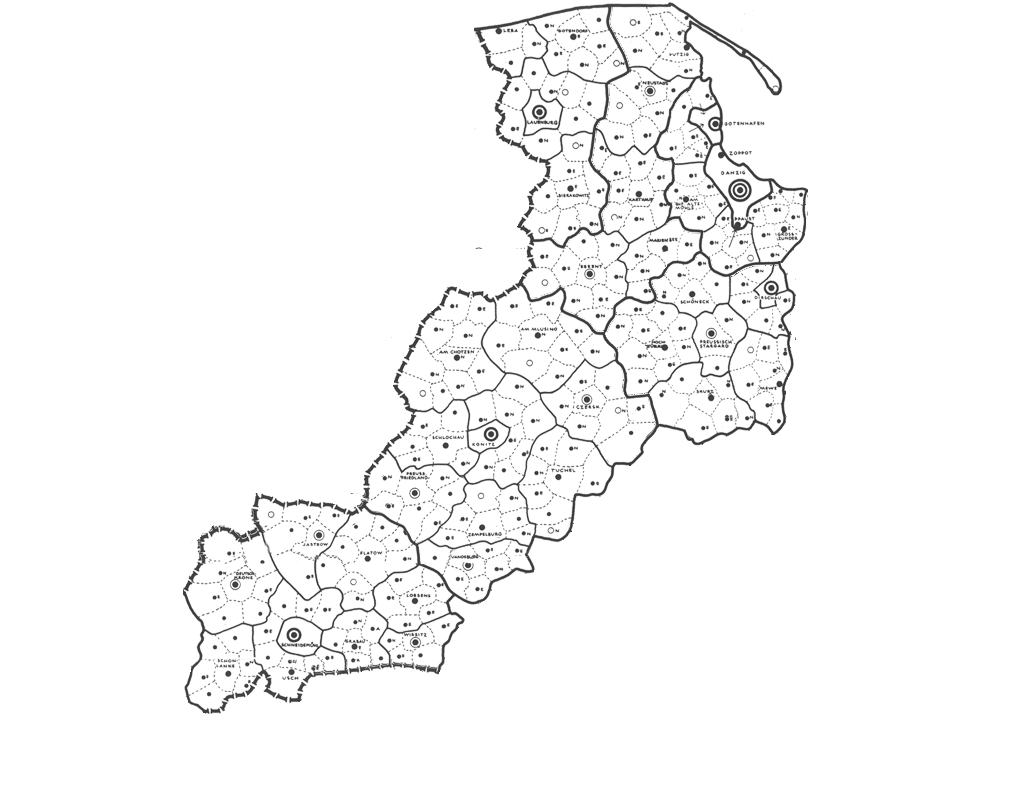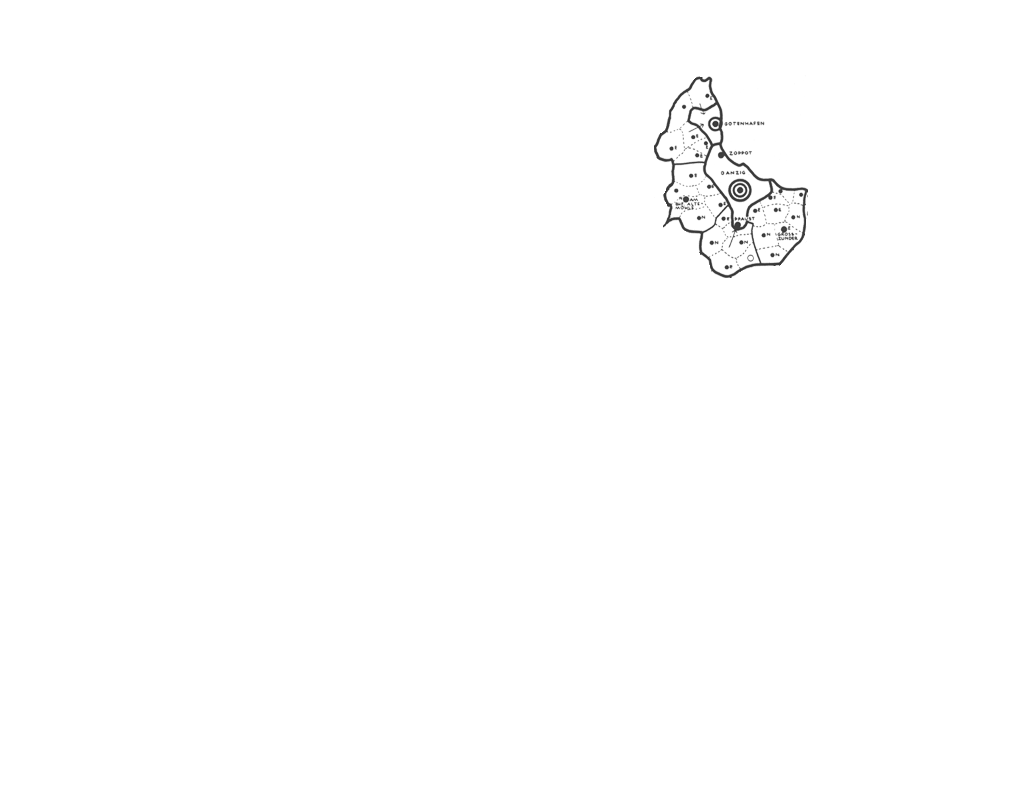Figure 6.a.  Danzig--2.7 million region disassembled into smaller 210,000 regions.


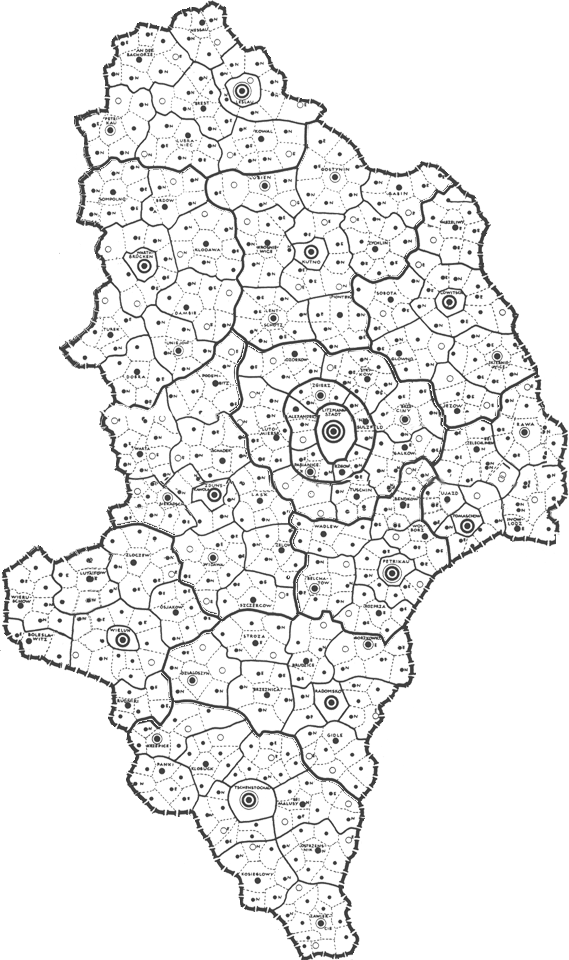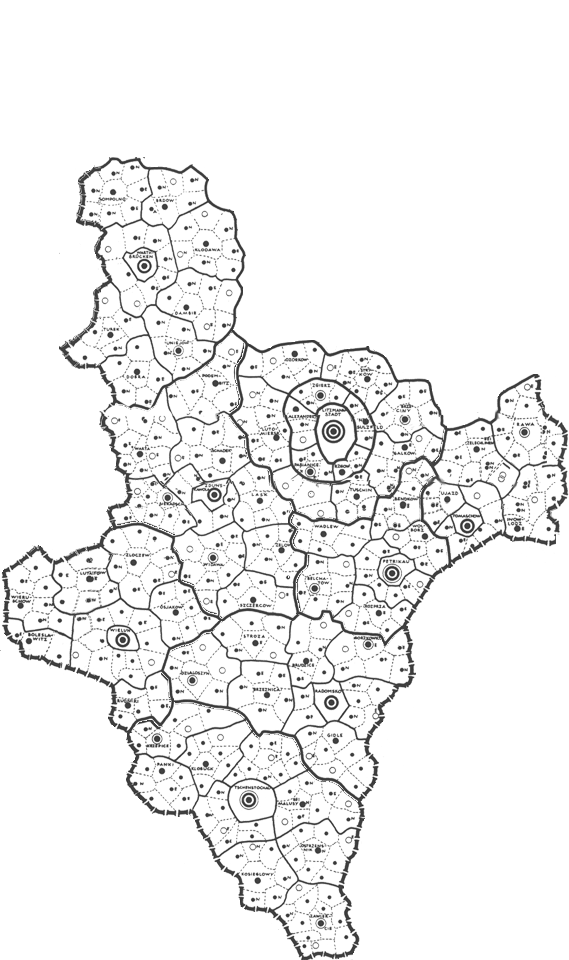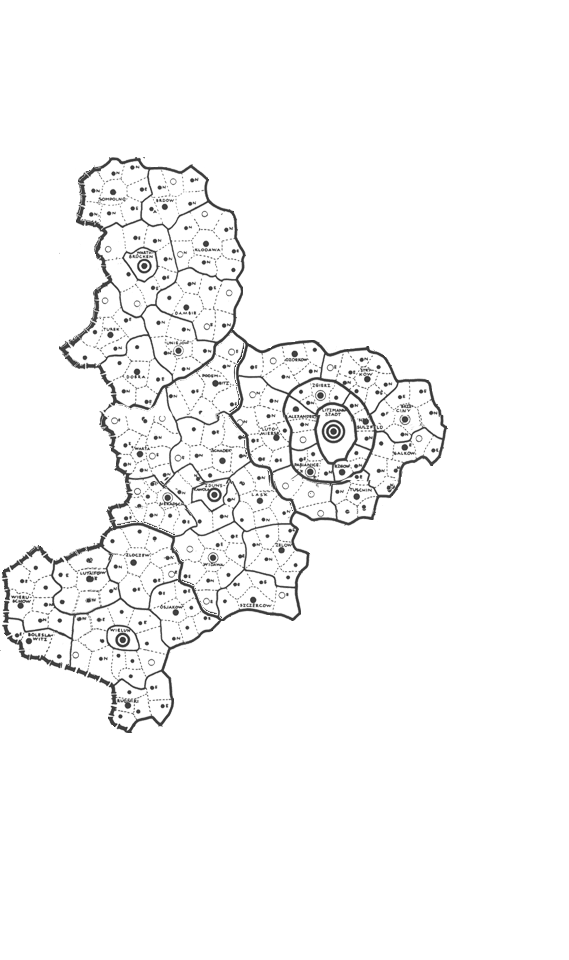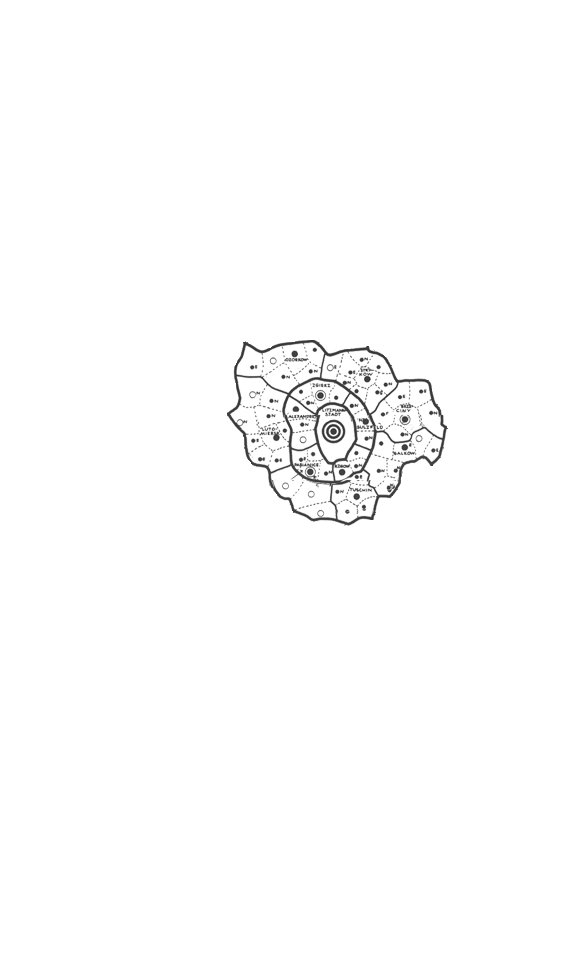Figure 6.b.  Litzmannstadt--2.7 million region disassembled into smaller 210,000 regions.


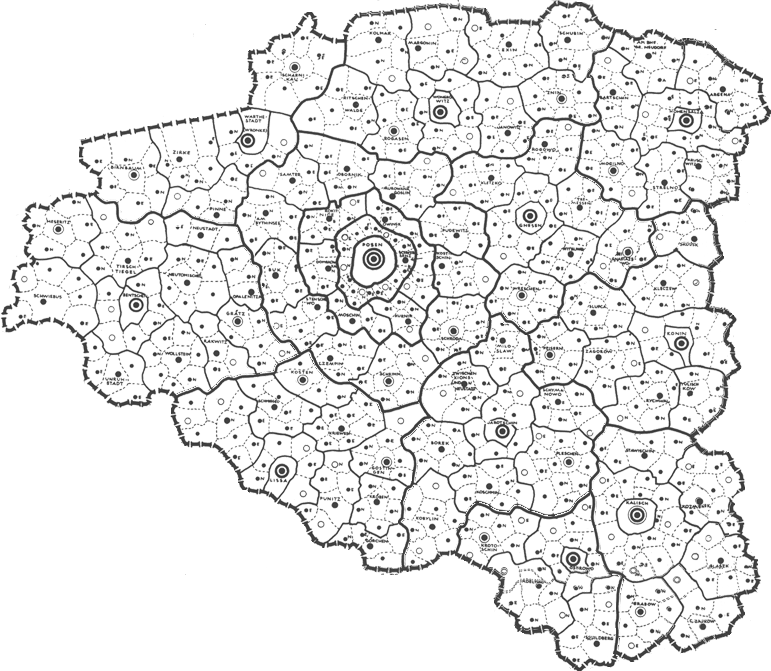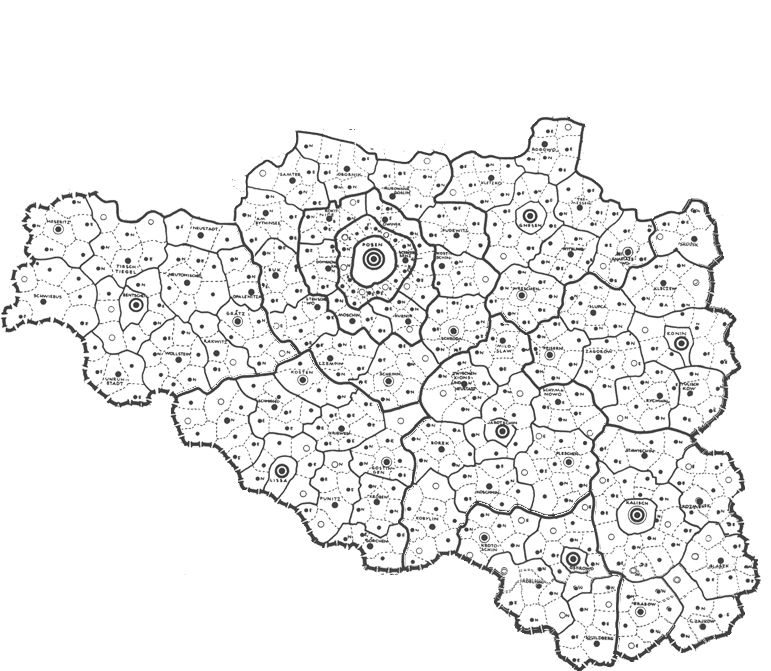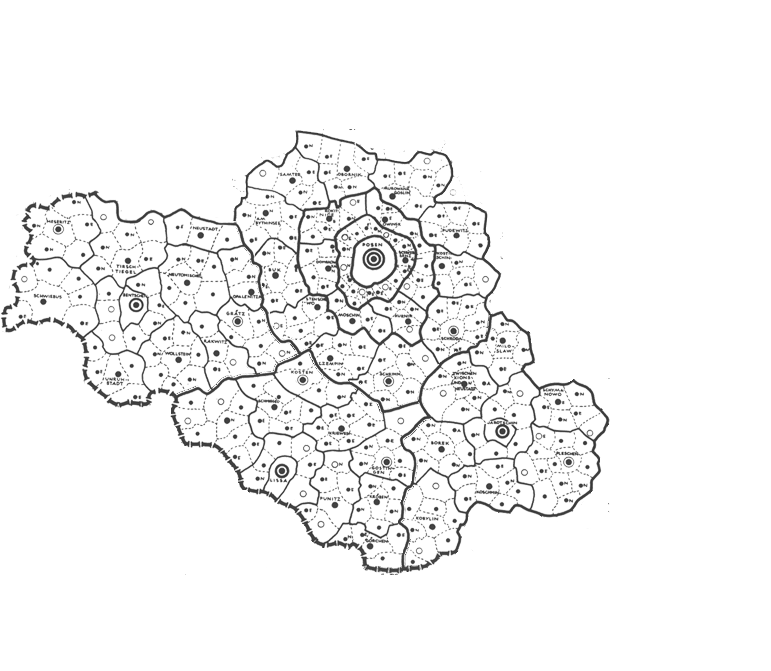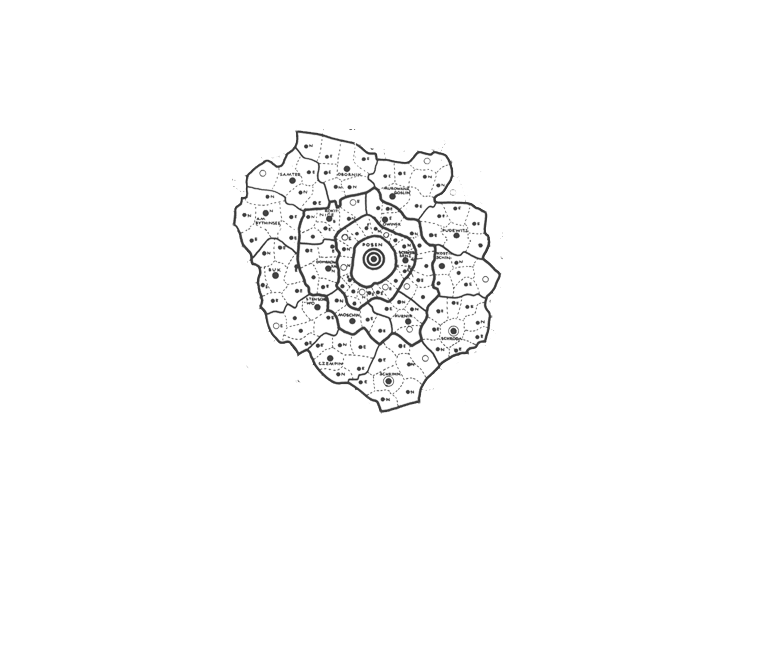Figure 6.c.  Posen--2.7 million region disassembled into smaller 210,000 regions.


The focal point of each of the 210,000 regions is assigned to the corrresponding benchmark.  One of these regions has a blue rod as focal point, others have red rods as focal points, and yet others have gold rods as focal points.  There is no instance, in the case of the full regions, of assigning more than one rod to a 210,000 region; in addition, the entire set is used.  Thus, all blue rods, all red rods, and all gold rods (with none omitted) necessarily fit these three reassembled 2.7 million regions.  They are shown in Figure 7: the fit is true on the rods with distortion and error increasing away from them.



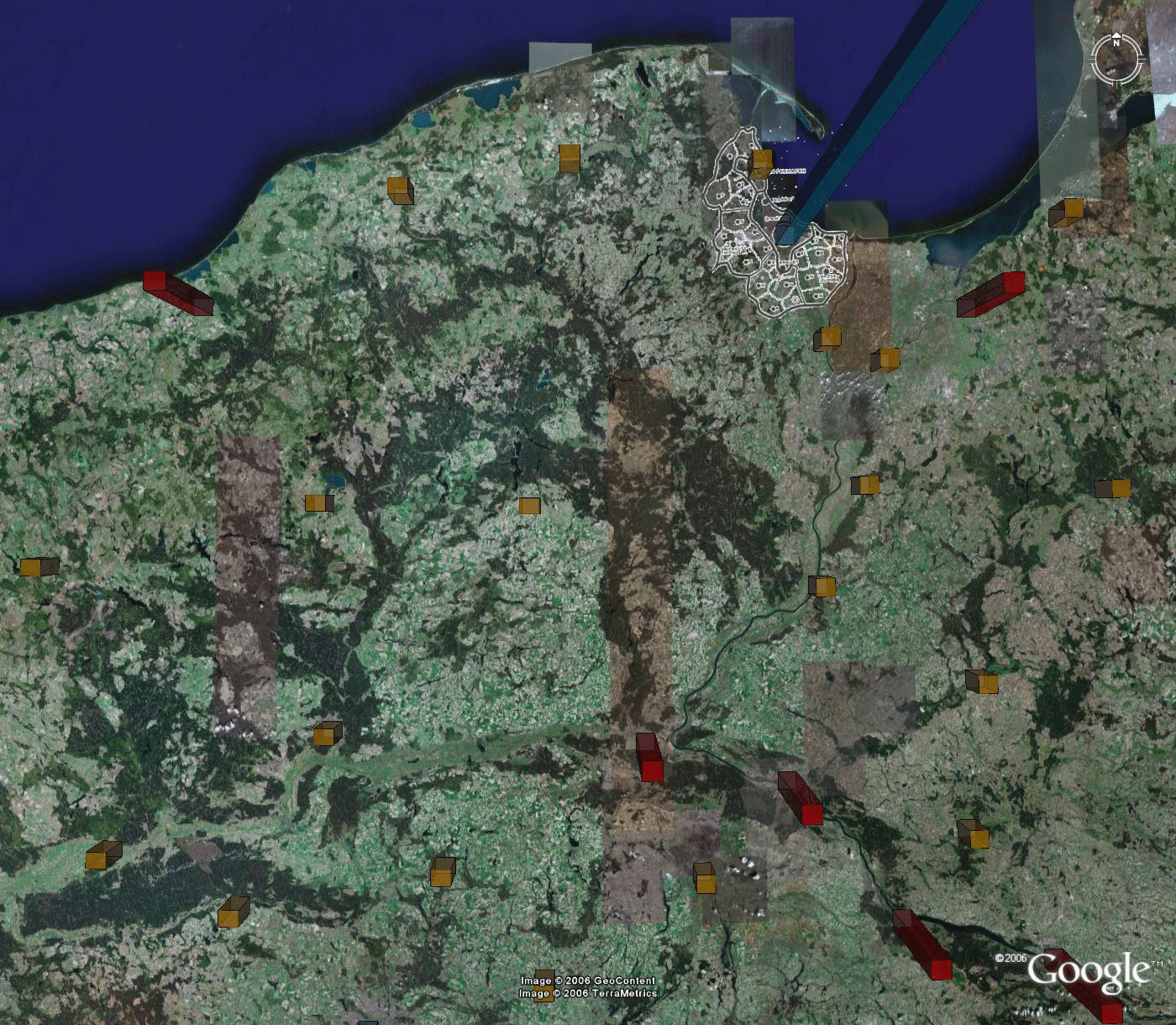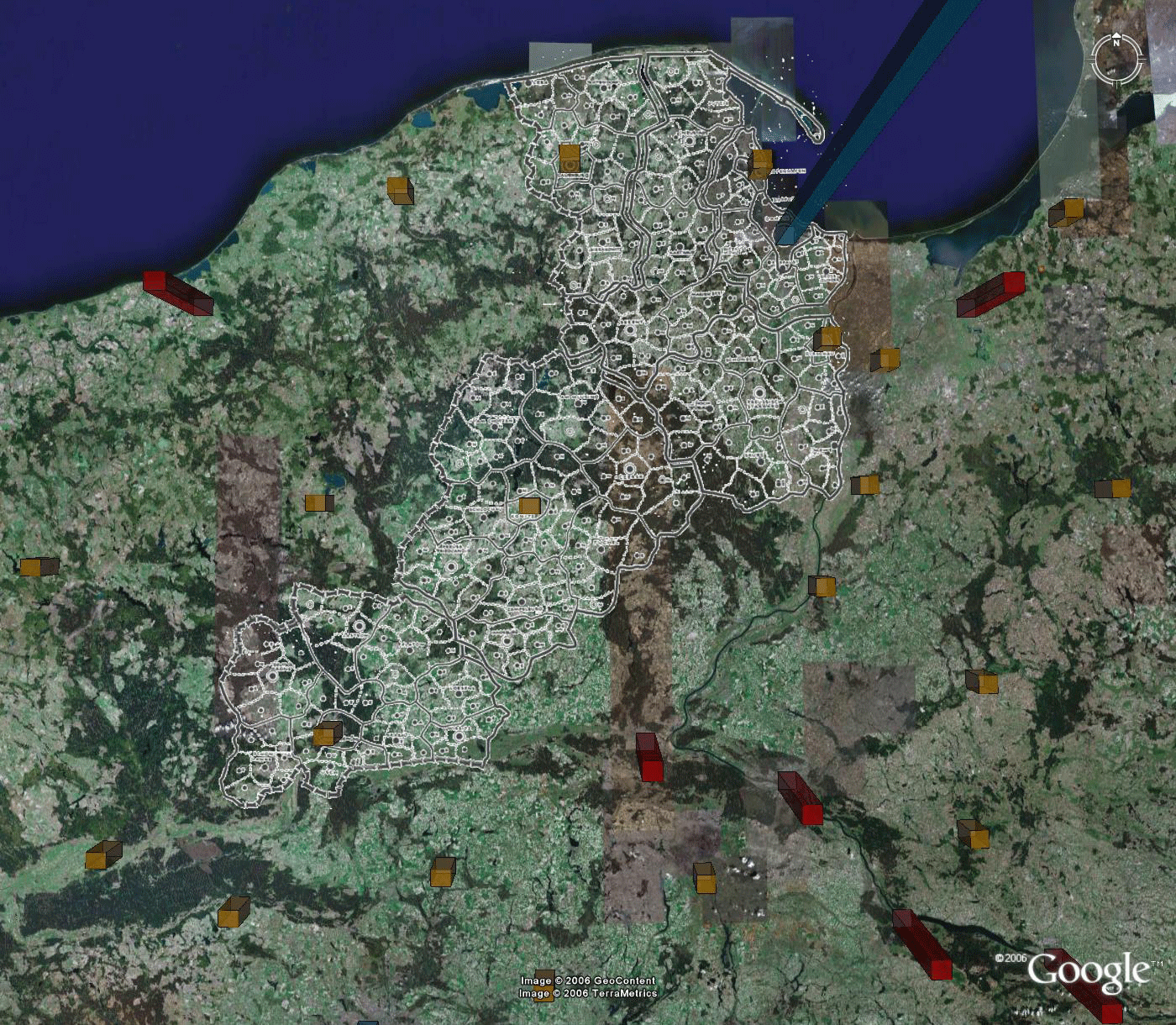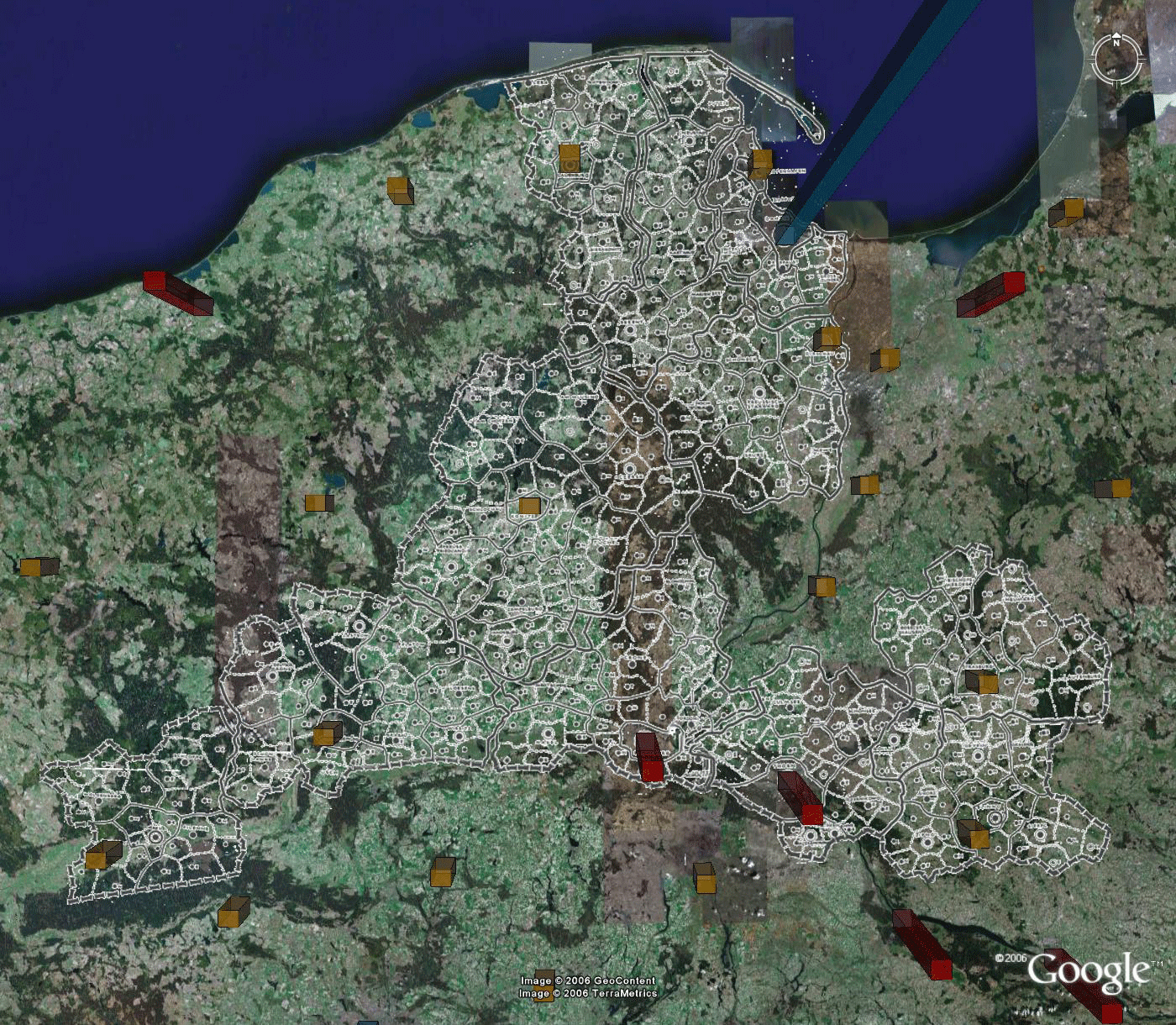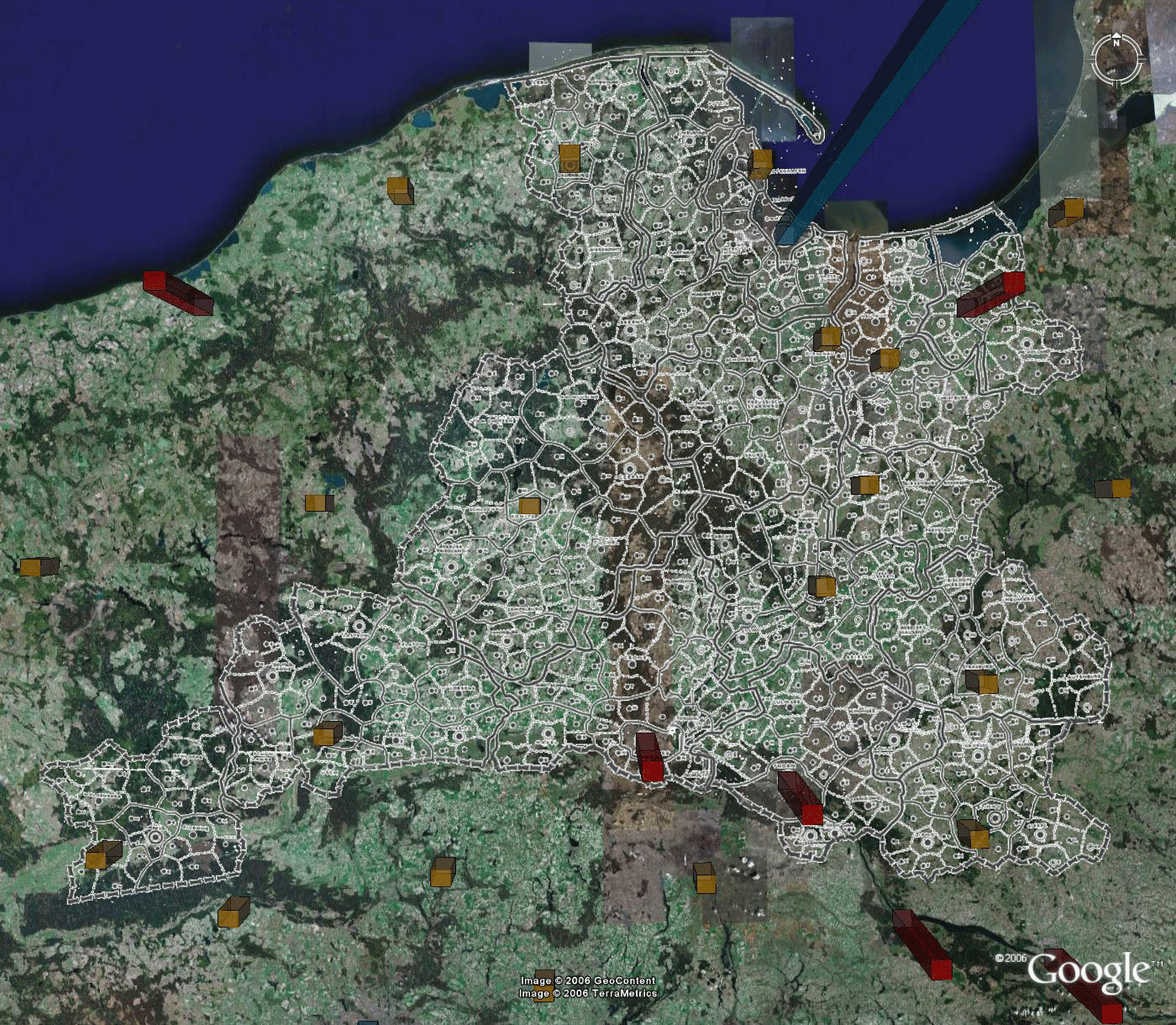Figure 7.a.  Christaller's 2.7 million Danzig region formed from 210,000 regions assigned to benchmarks.


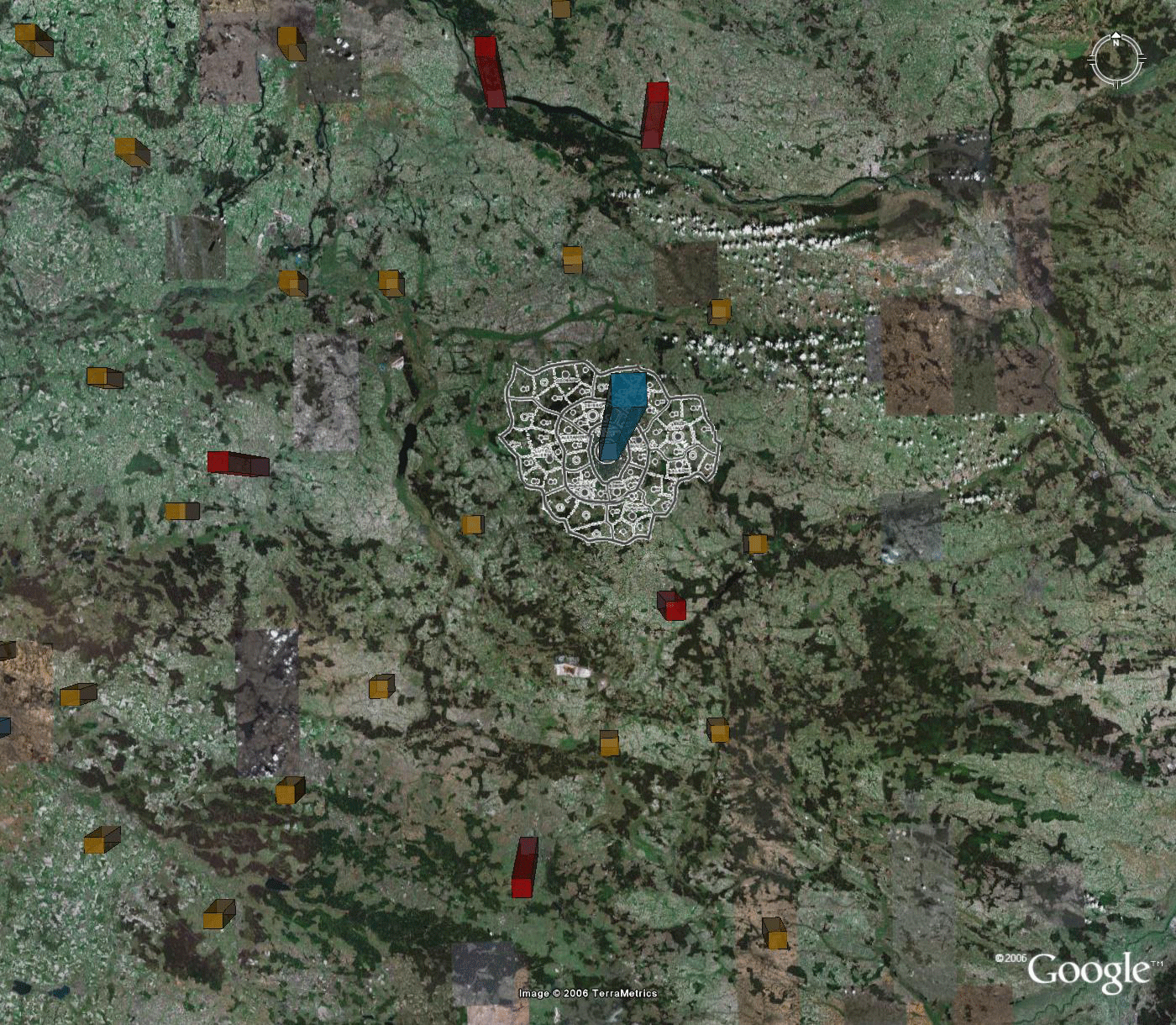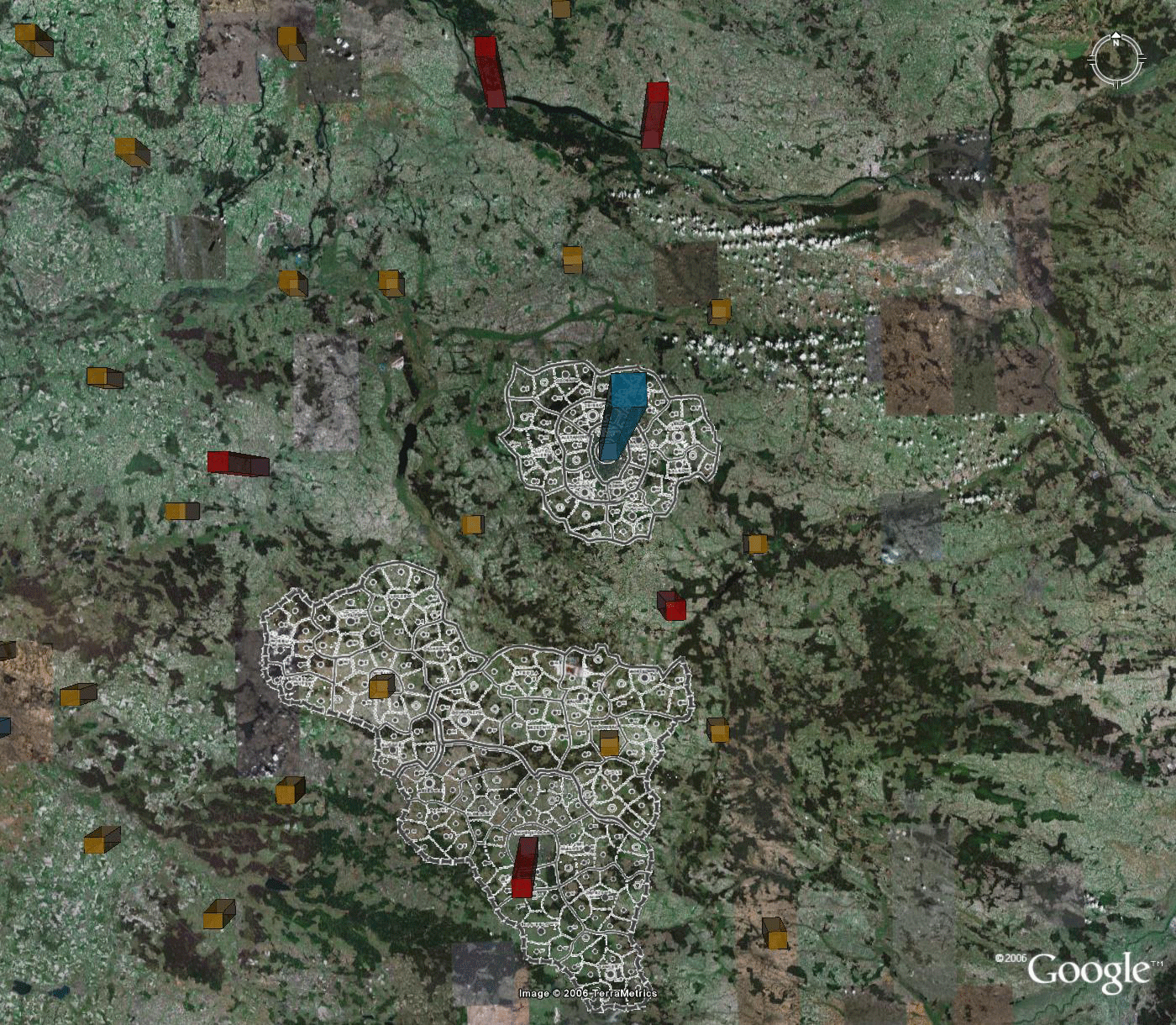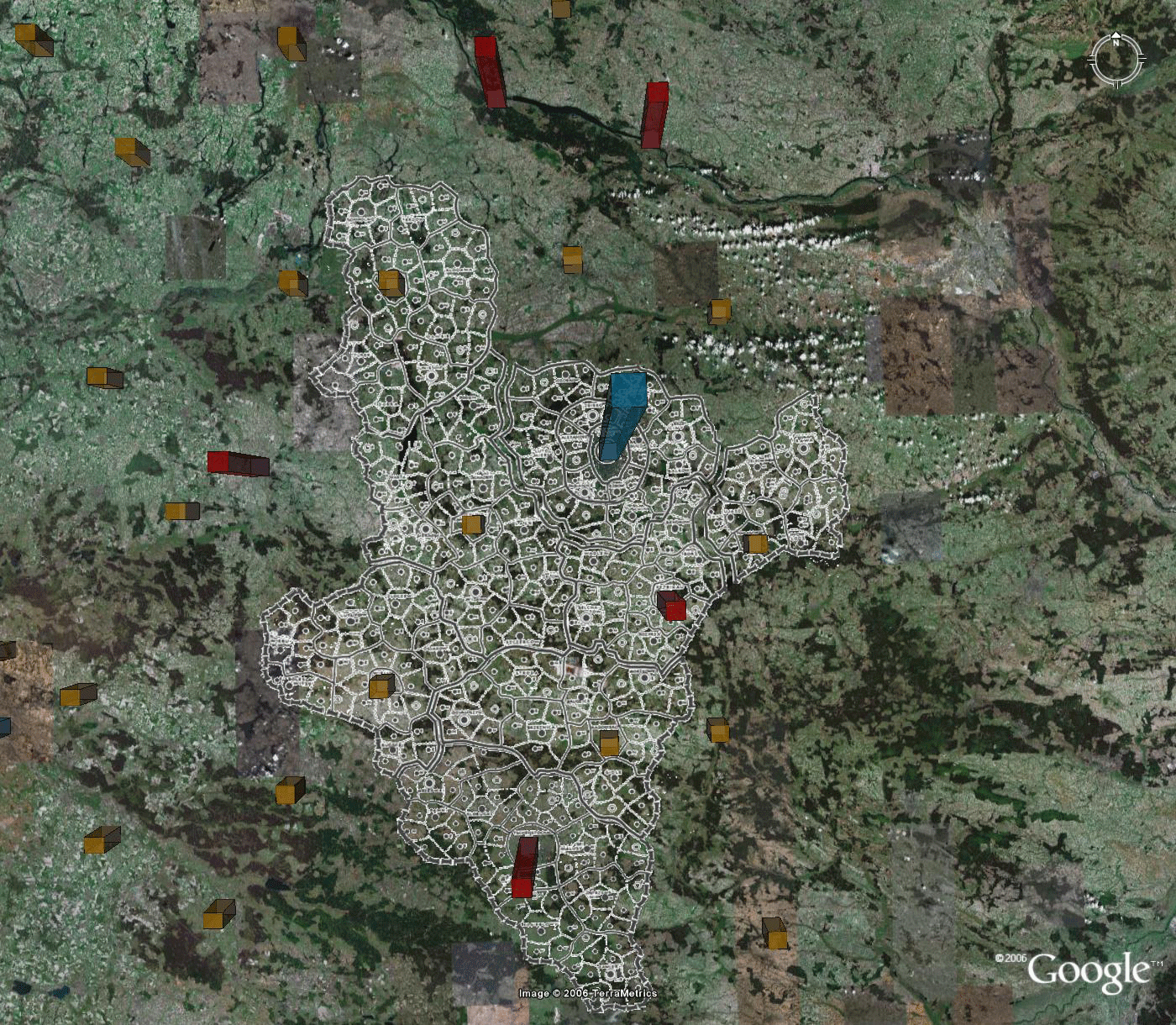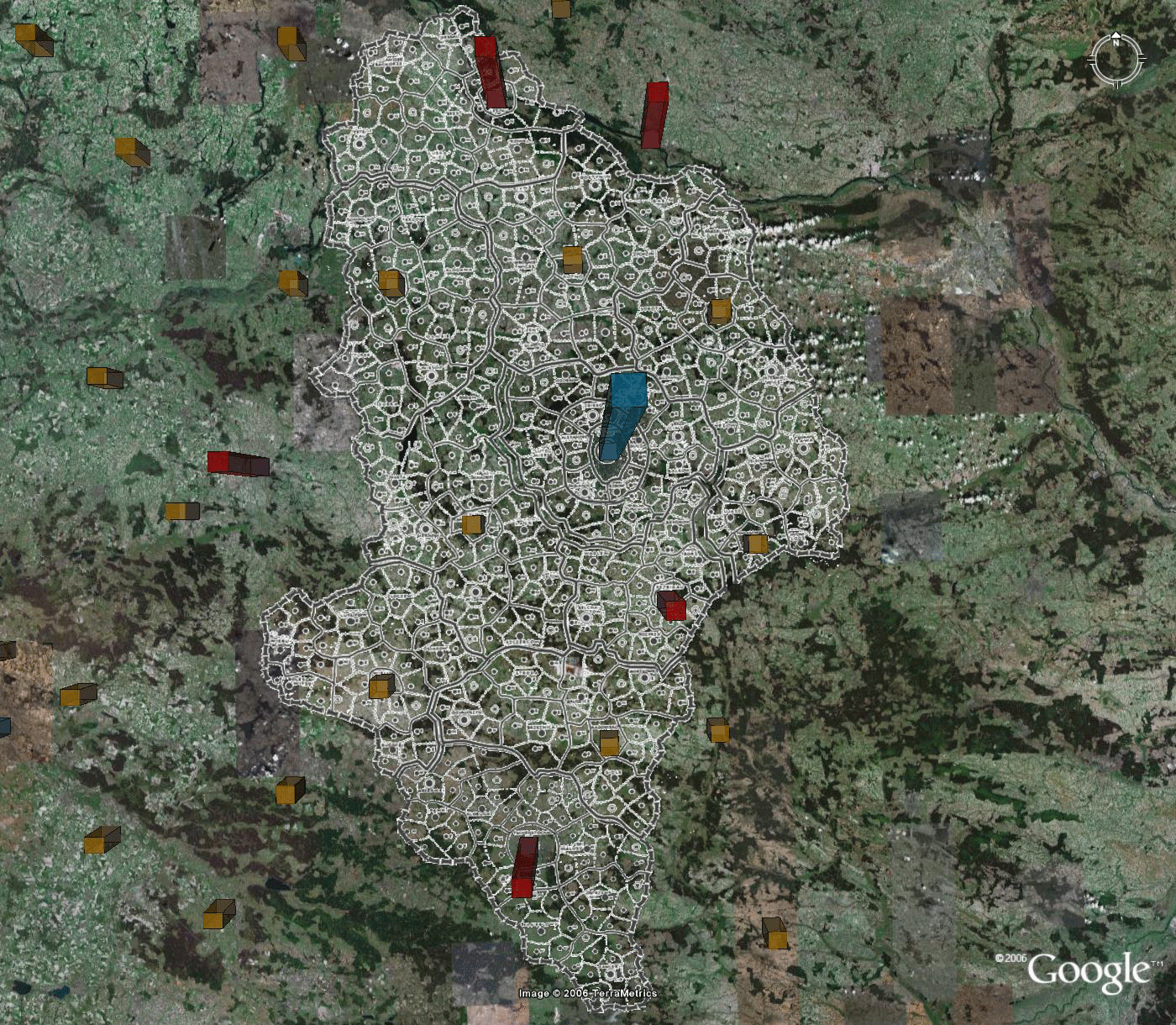Figure 7.b.  Christaller's 2.7 million region Litzmannstadt formed from 210,000 regions assigned to benchmarks.


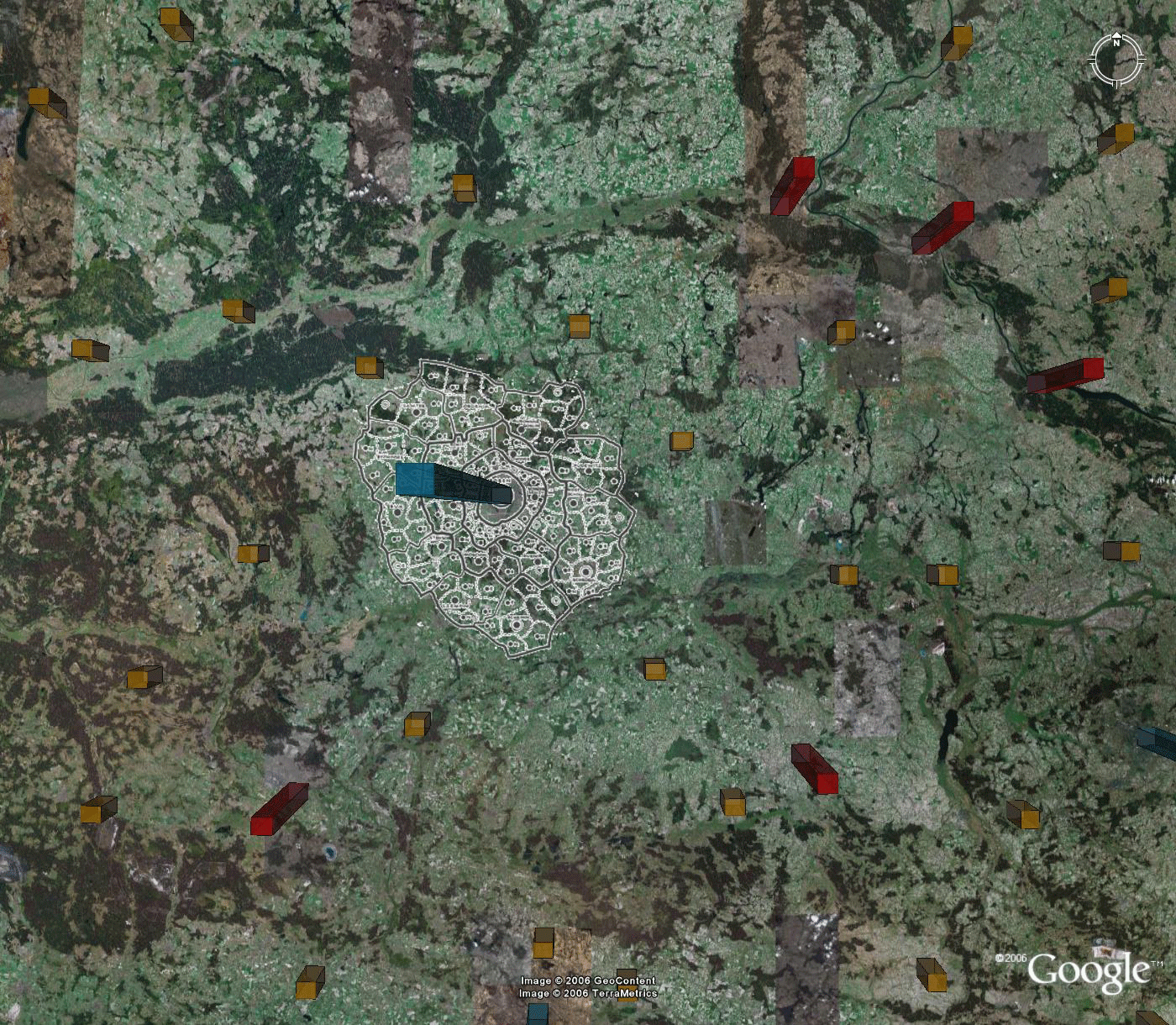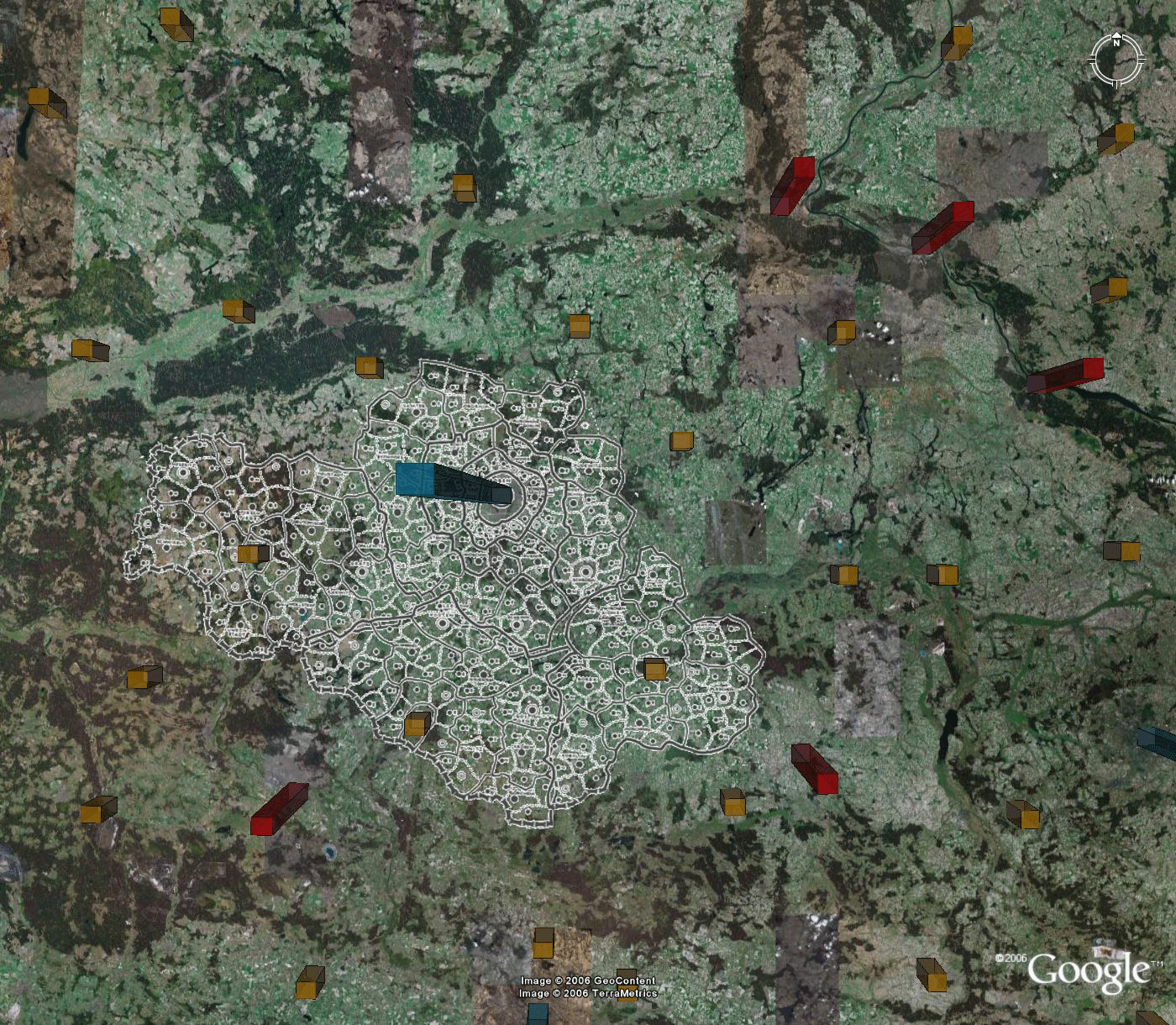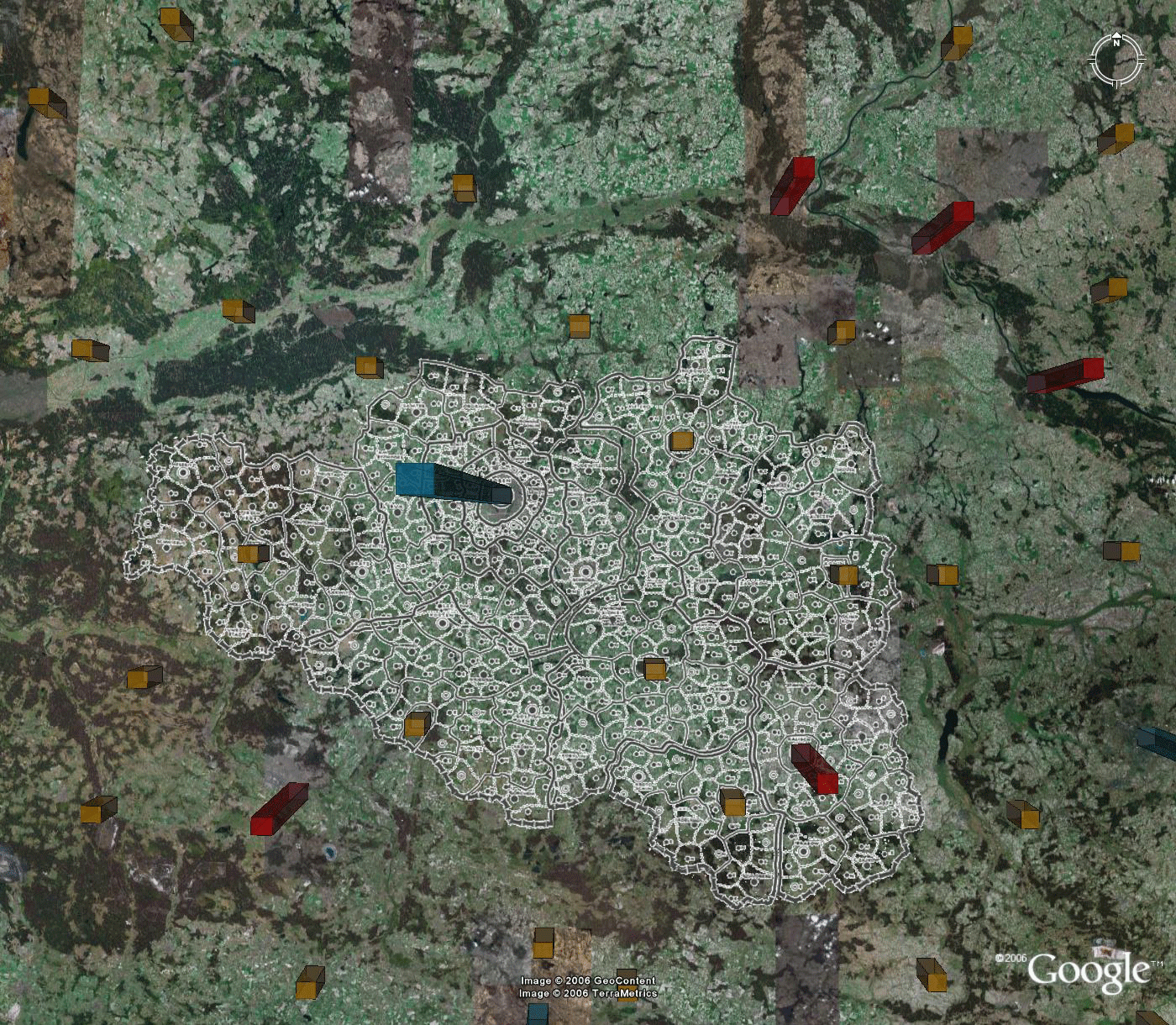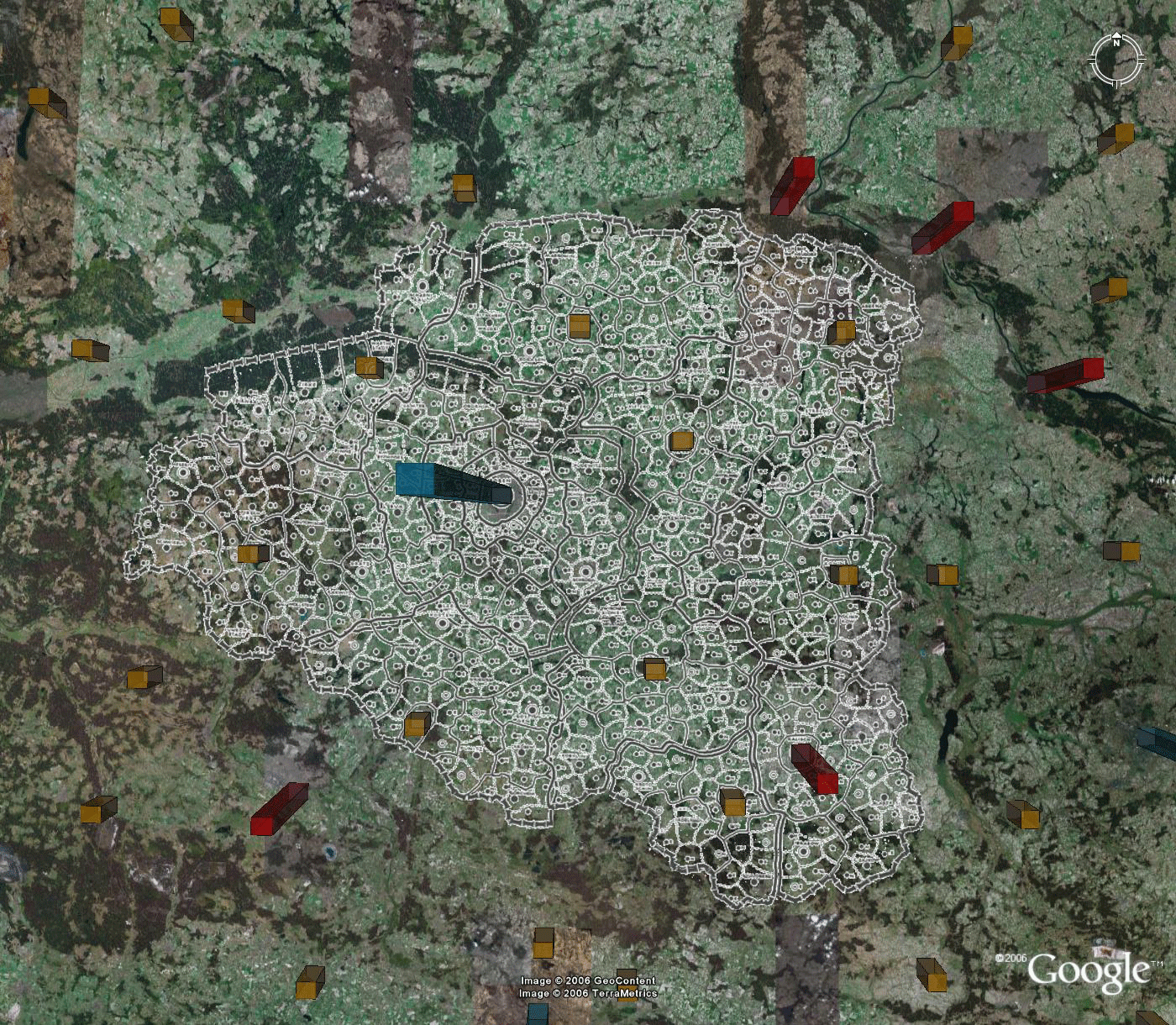Figure 7.c.  Christaller's 2.7 milion region Posen formed from 210,000 regions assigned to benchmarks.


The Reassembled Full Map

In addition to the three full regions of Danzig, Posen, and Litzmannstadt, there are two incomplete perimeter regions, one to the east and one to the west, as well as regions centered on Breslau, the Katowice region, Krakow, and Stettin.  They too were processed, as above, to force the blue, red, and most gold rods to fit the Christaller map. Only in the Katowice region, near the bottom of the map, was there any lack of fit:  in that region a red rod is the focal point and in addition there are a number of gold rods also within the same boundary as the red rod.  Because that region is small in extent, the error in gold rod placement is also small but increases with distance from the red rod.   Finally, all of these regions were reassembled on the Google Earth globe.  The result is shown in Figure 8.  All blue and red fit exactly.  Most gold rods also fit exactly (except those in the Katowice region).  Error is distributed across the map, away from benchmarks.  It is also evident at the edges of the map.  The fit of the map using smaller regions is superior to any other considered.  Again, the reader has all files available to replicate results:  to see the terrain in relation to the Christaller map, to drive around through it, to study point location patterns from various perspectives, to visualize the landscape, to turn layers off and on, and to make history and associated policy issues come alive.


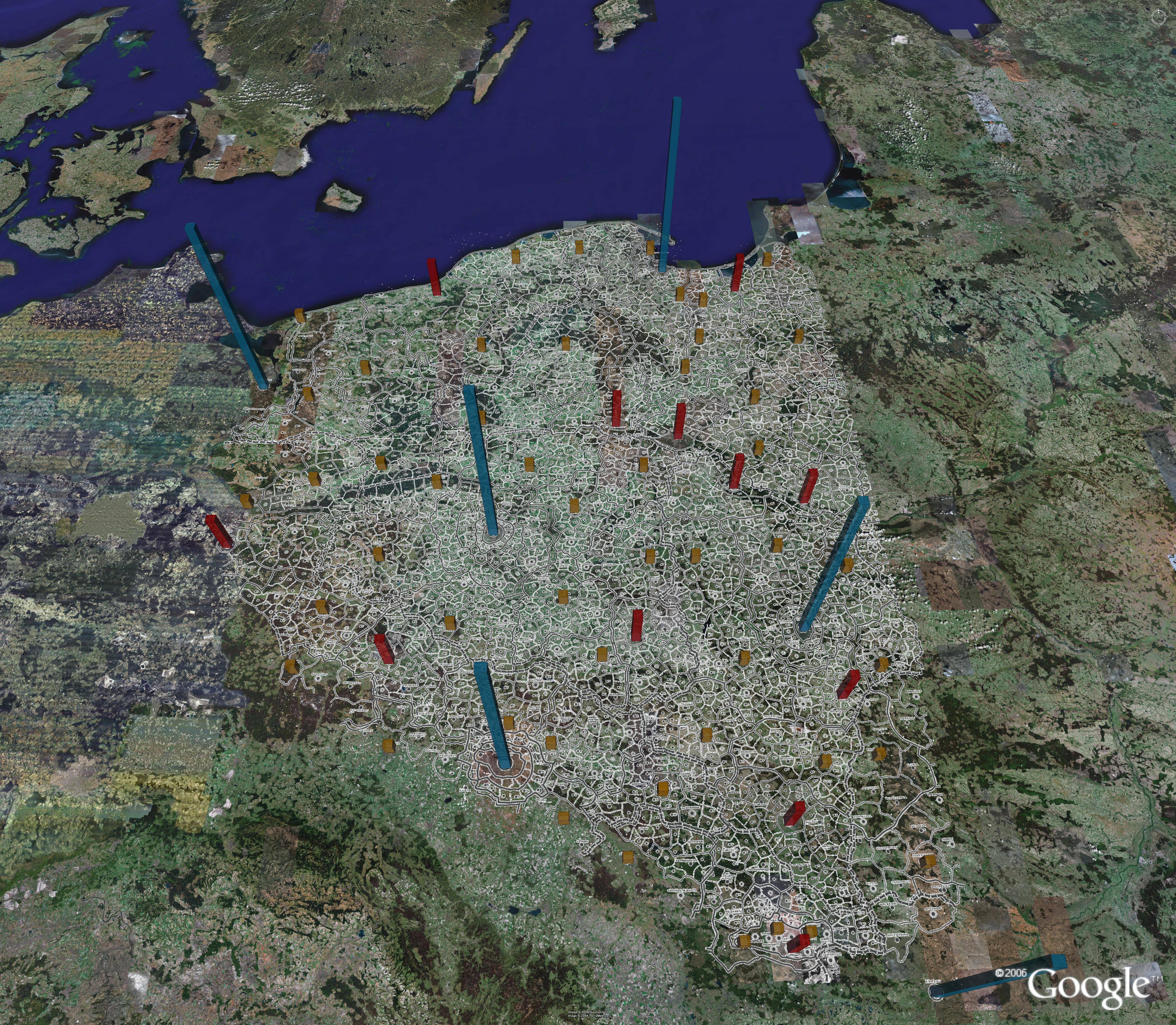Figure 8.  The reassembled map.  The Christaller map now fits the blue, red, and most gold rods of the virtual world.  Error increases away from these rods and at the map perimeter.

The Future
RELATED REFERENCES  [All links last accessed on Nov. 27, 2006.]
Solstice:  An Electronic Journal of Geography and Mathematics, Volume XVII, Number 2
Institute of Mathematical Geography (IMaGe).
All rights reserved worldwide, by IMaGe and by the authors.
Please contact an appropriate party concerning citation of this article: sarhaus@umich.edu
http://www.imagenet.org
Hillingdon Harrow Barnet Brent Enfield Ealing Hammersmith and Fulham Hounslow Richmond upon Thames Kingston upon Thames Merton Sutton Croydon Bromley Bexley Havering Redbridge Waltham Forest Barking and Dagenham Haringey Newham Greenwich Lewisham Southwark Lambeth Wandsworth Kensington and Chelsea Westminster City of London Tower Hamlets Camden Islington Hackney