Making It Clear:  The Importance of Transparency

Sandra Lach Arlinghaus

Part I:  Escher/Barr Earth


INTRODUCTION

Escher's art in the "Circle Limit" series shows interdigitated pattern realized inside a circle with the repeating pattern shrinking as one moves outward from the center of the circle.  In his correspondence with the geometer H. S. M. Coxeter, one sees the emergence of these figures.  The Poincare Disk representation of hyperbolic geometry is apparently what Escher was employing in representing repeating pattern veering off to infinity...a compact and bounded infinity rather than the usual unbounded one that lurks in our Euclidean-only trained minds.

In "The Animated Pascal," an early Escher screen capture was superimposed on Google Earth, suggesting how a Circle Limit image might look when wrapped around a sphere--much like reprojecting a map back to the globe.  While the result is interesing as a visual representation, it does not really show what would happen had the Circle Limit series actually been drawn on a spinning globe.  One might suppose, that had such drawing taken place, that all polygons would have had identical size.  As one approched what had been the horizon, at first glance, that the seemingly small polygons on the initial horizon would emerge as full-sized as the observer drew nearer to them.  As we know, a change in vantage point often reveals differences in space and time.

UNMASKING THE GOOGLE GLOBE

To look at a drawing on a spinning globe, consider using the globe from Google Earth.  All that would be needed is to figure out how to remove the images forming the Earth.  Figure 1 illustrates how to do so.   The initial frame of the animation shows the Google Earth globe with continents, oceans, and so forth.  The second frame shows the graticule placed on the globe of continents.  To activate the graticule, go to View | Grid in the pull-down menus at the top.  Finally, remove the continental skin.  The third frame shows highlighting of the layer "Primary database" in the Layers box on the left.  In the fourth and final frame, the slider in the "Places" box, at the bottom is moved all the way to the left.  This action causes the continental skin covering the globe to be obscured.  Now, the Google Earth globe of the Earth, its landmasses and oceans, has been converted to a blank sphere with a graticule.  (For user-control of the animation sequence, click on this link to a movie of that sequence.)

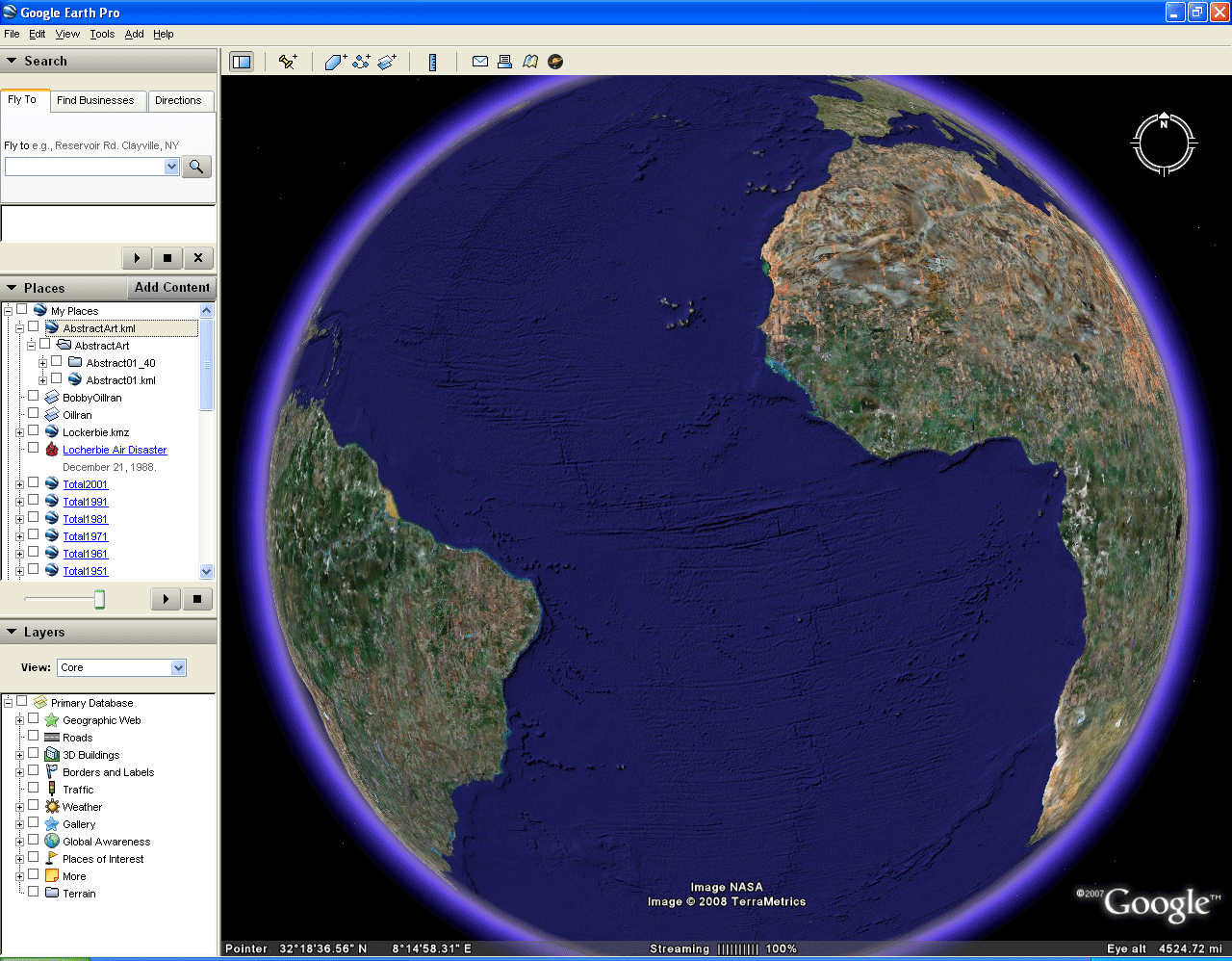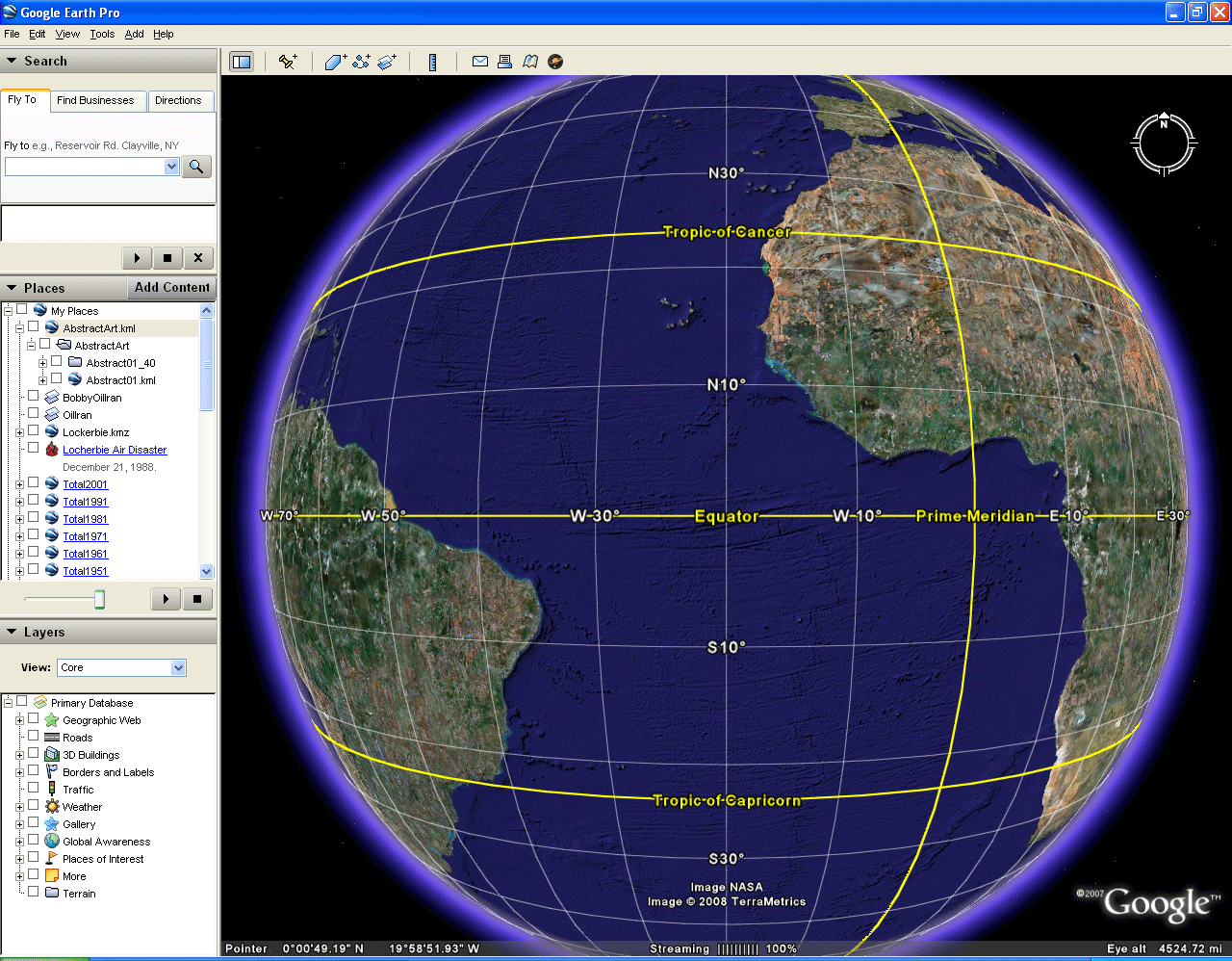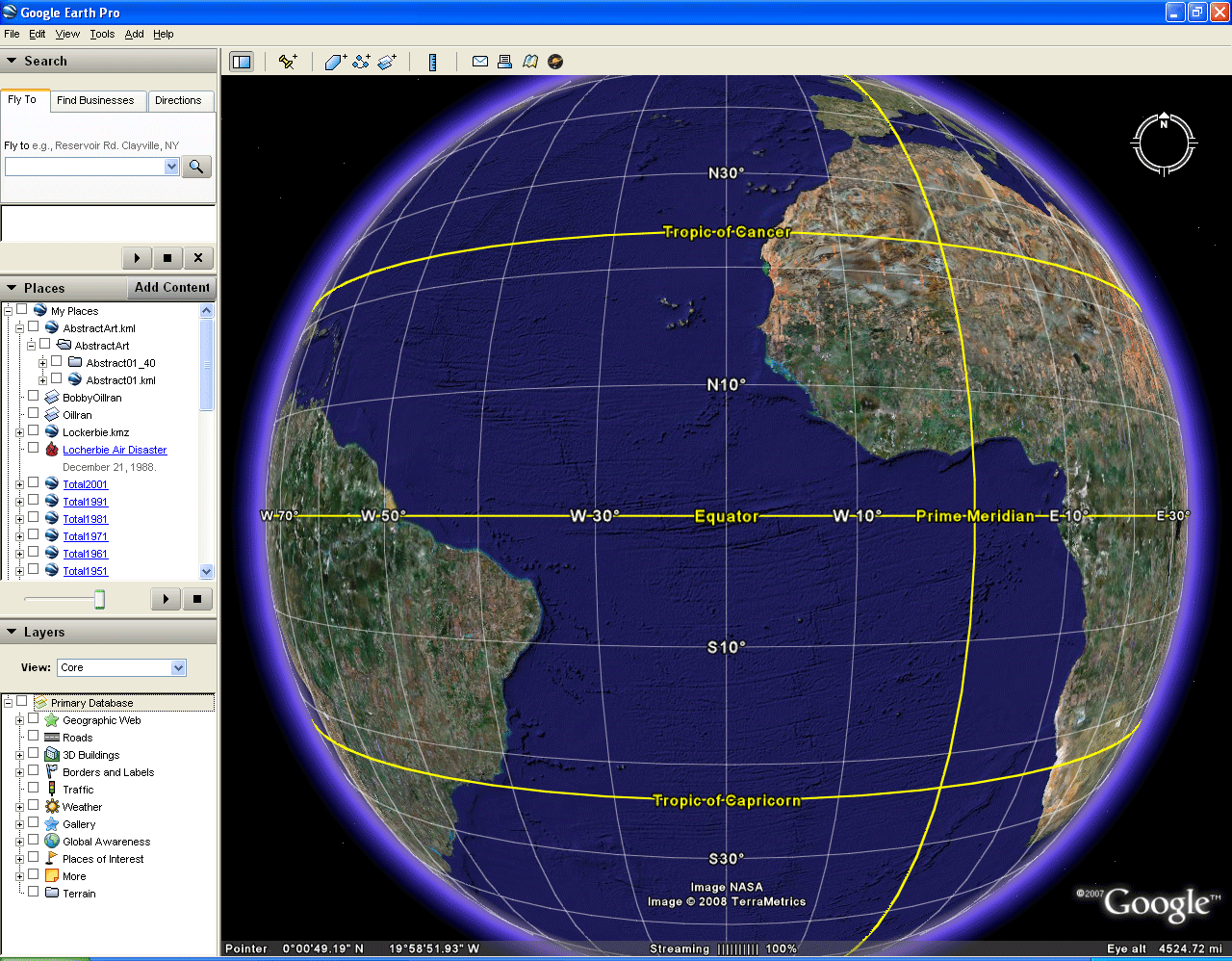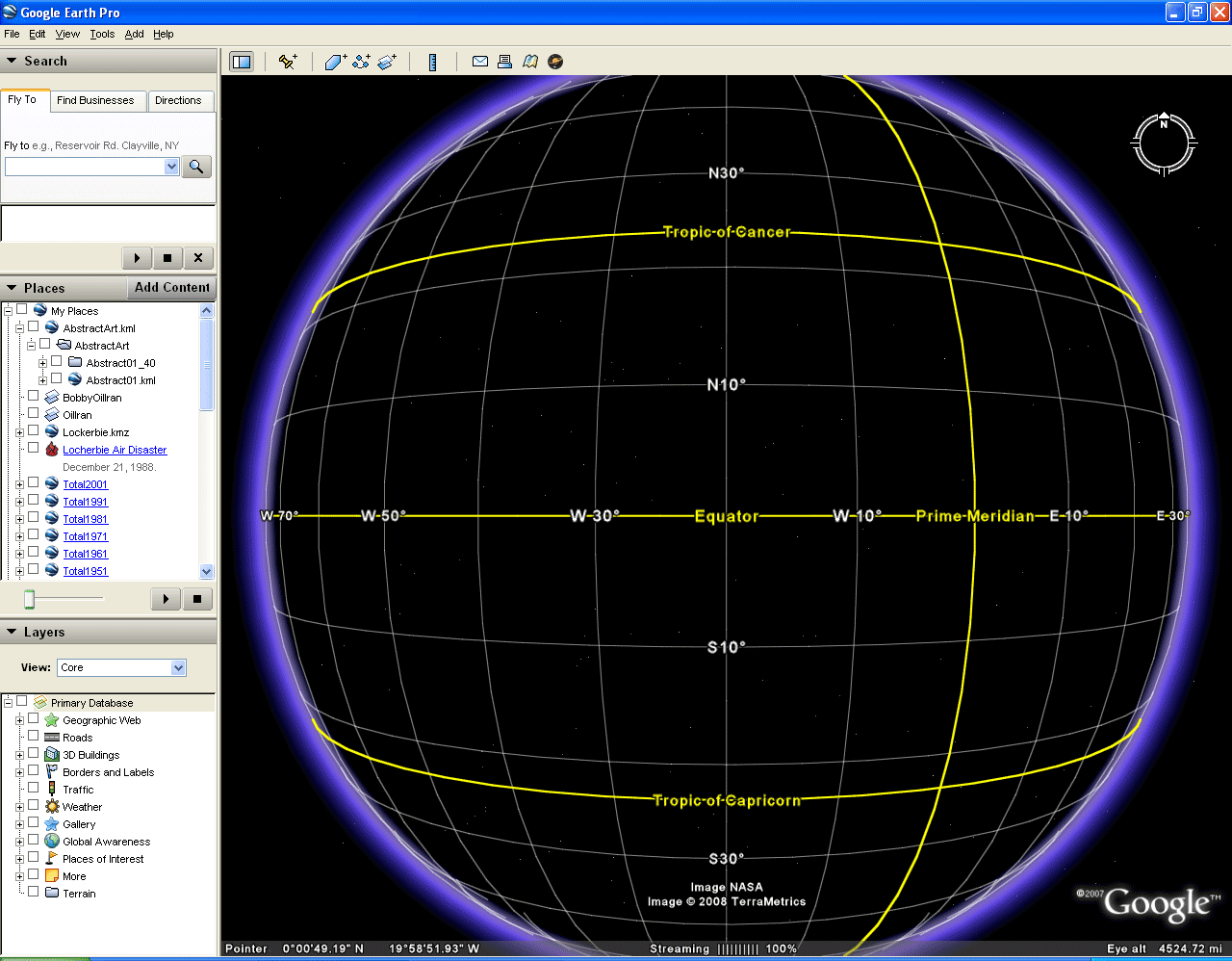Figure 1.  Unmasking the Google Globe.

INSERTING ABSTRACT ART ON THE GOOGLE GLOBE

In Figure 2, a simple repeating self-similar pattern is drawn using the lines of the graticule.  As one zooms in on the Google Earth graticule, finer partitions of latitude and longitude emerge so that one can continue making smaller pattern.  The sequence in Figure 2 illustrates how one might execute such a process.

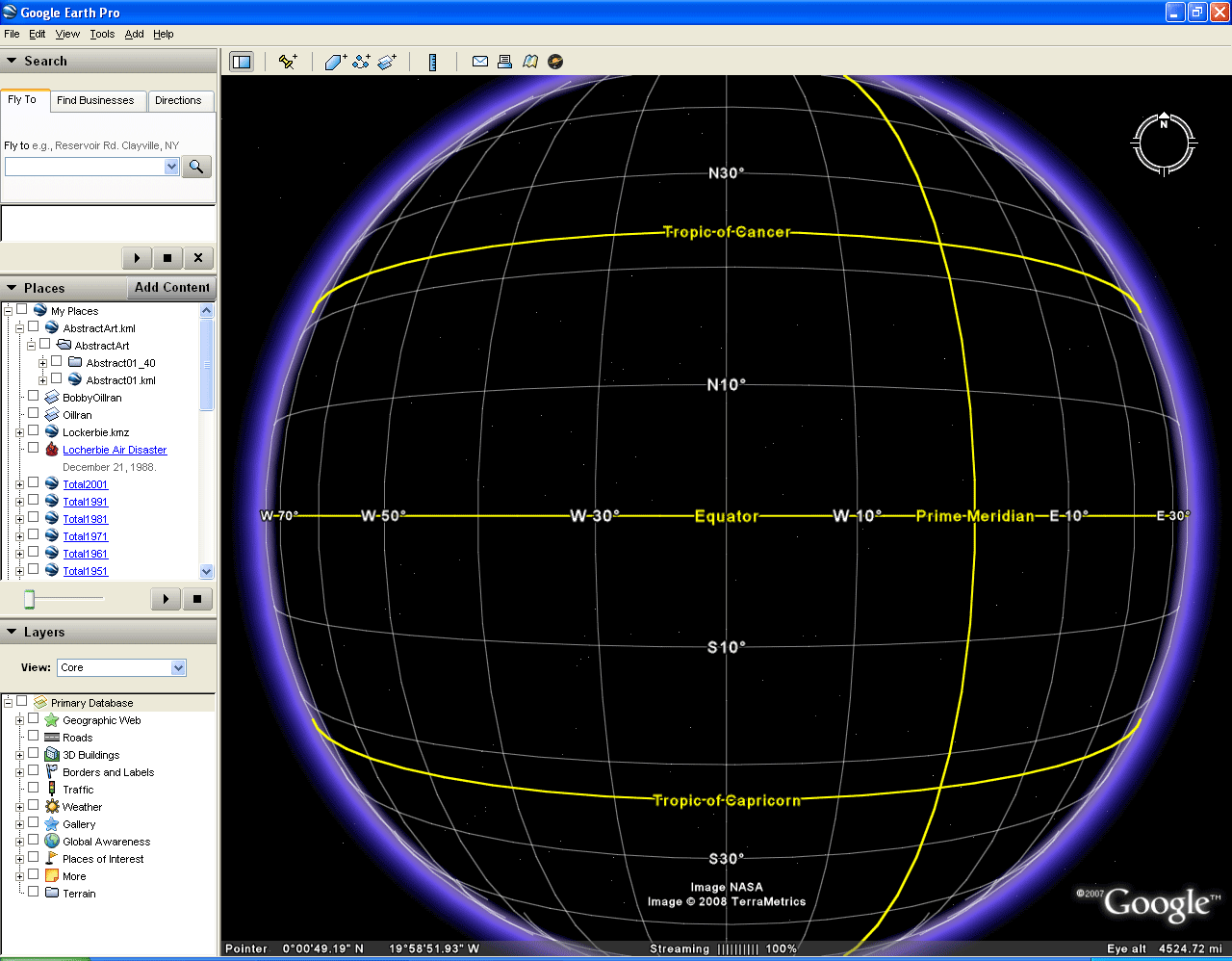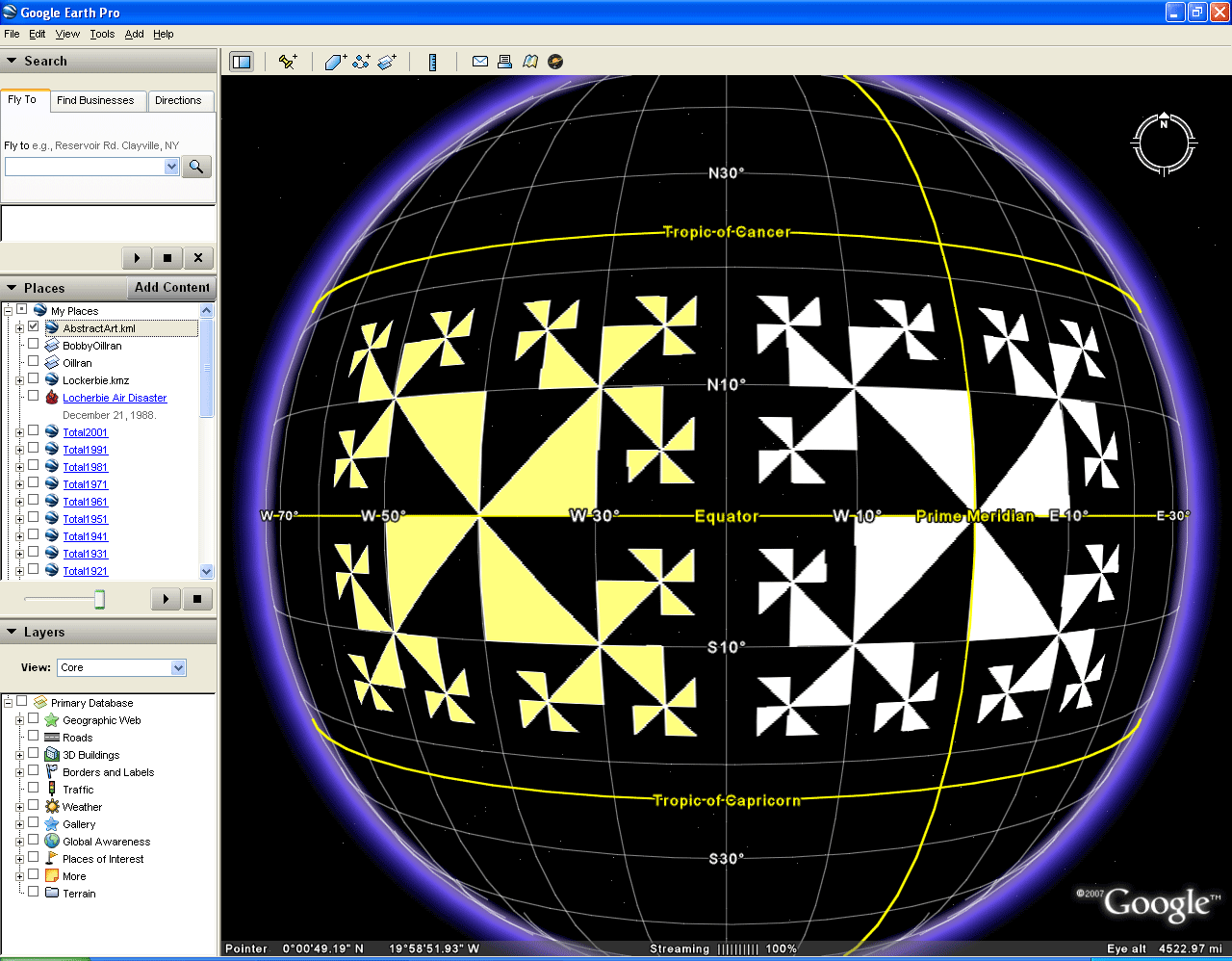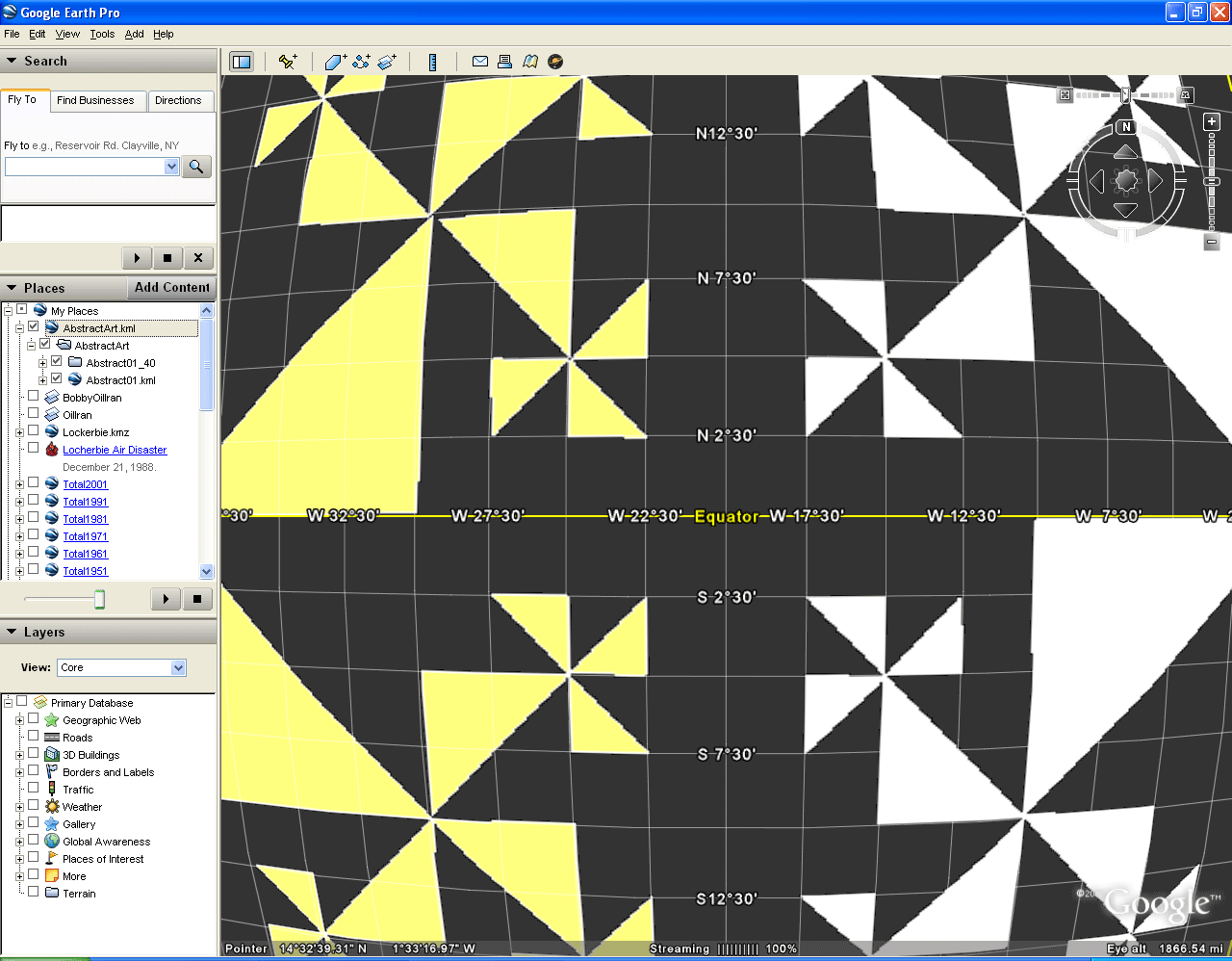Figure 2.  Inserting Abstract Art on the Google Globe.


TRANSPARENCY OF THE GLOBE

What is unclear from Figures 1 and 2 is whether one can look "through" the globe or whether the globe still has a skin on it.  When the Google Globe, with pattern from Figure 2, is set to spinning mode (drag it), one sees clearly that the globe itself is transparent.  Watch as the generated pattern spins around a great circle in Figure 3 in an animated sequence of screen captures from Google Earth.  Download the associated .kml flie linked here and try it yourself in Google Earth.

Figure 3.  Transparency of the globe. 


TRANSPARENCY OF THE PATTERN:  ECLIPSING THE GOOGLE GLOBE

The globe itself is transparent.  It appears, from the manner of construction that the white or yellow triangles of the pattern should be opaque and the uncolored black within the convex hull of the pattern should remain transparent.  Indeed, when the Earth's continental skin of continents and water is returned to the globe (Figure 4), along with the pattern, the triangles that were black now become blue (when over the ocean).  The return of the skin also blocks the view through the globe; the white pattern that appears on the back side of the globe in Figure 3 is completely blocked when the Earth skin, and even a very slightly opaque version of it is returned to the Google Globe.  Notice, in Figure 4, that when the pattern alone is viewed going around the edge of the globe, the black part of the pattern within the convex hull of the pattern (and a mat slightly beyond the hull) has become opaque and blocks out pattern behind it.  This observation accounts for gaps in viewing the pattern as it spins around the great circle of Figure 3.  To study this self-eclipsing effect of the pattern, consider viewing the animation as a movie in which the reader can control the animation speed. 


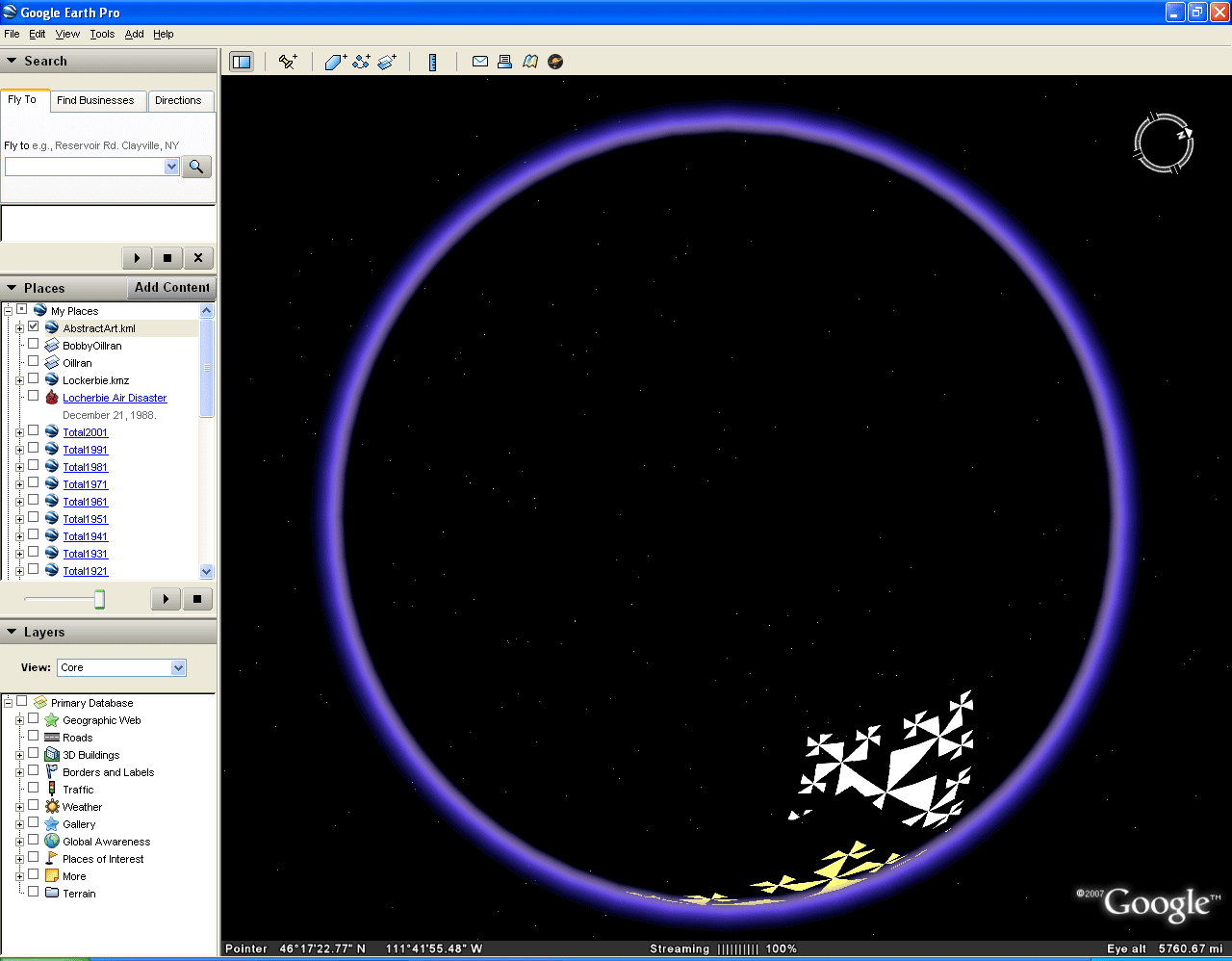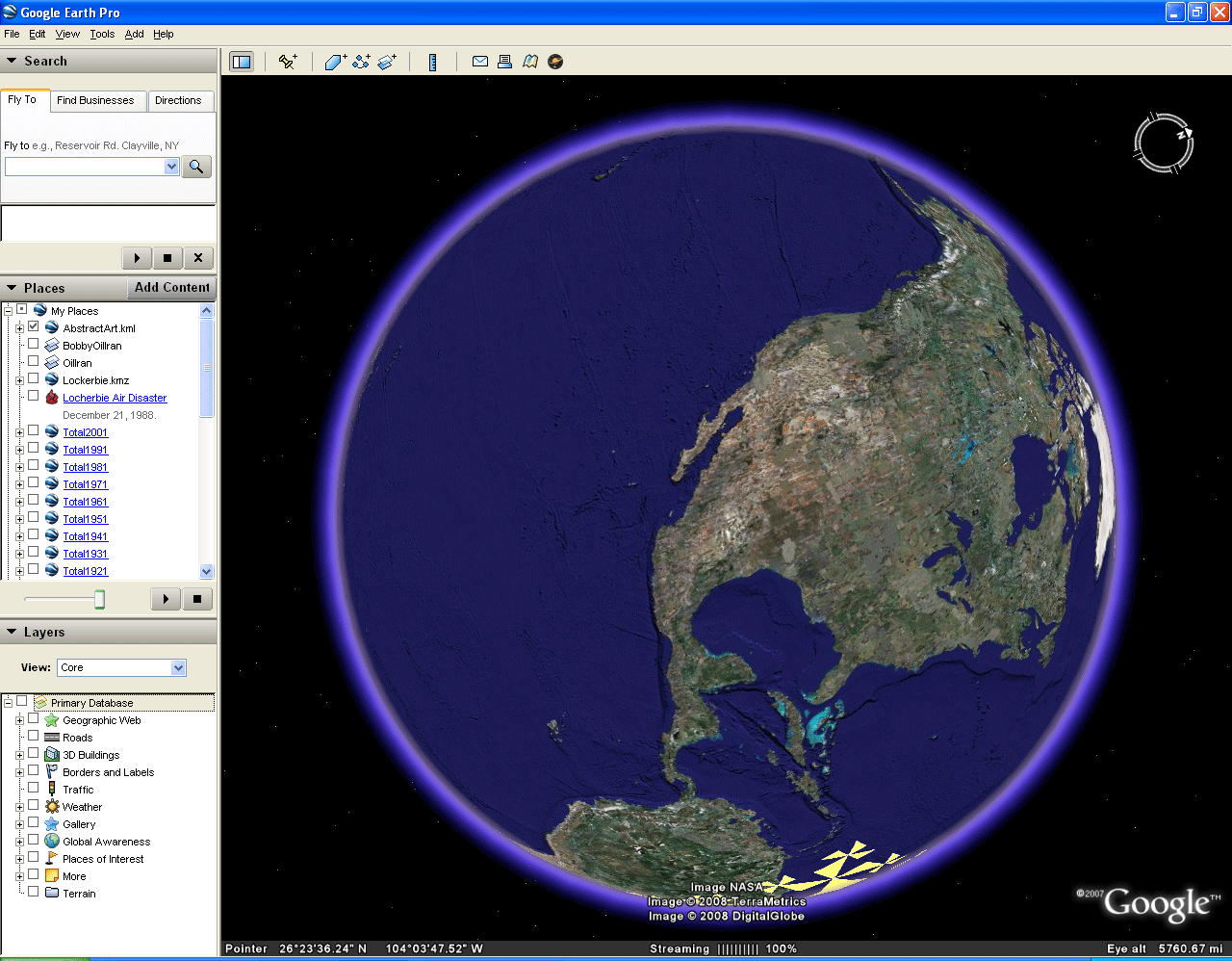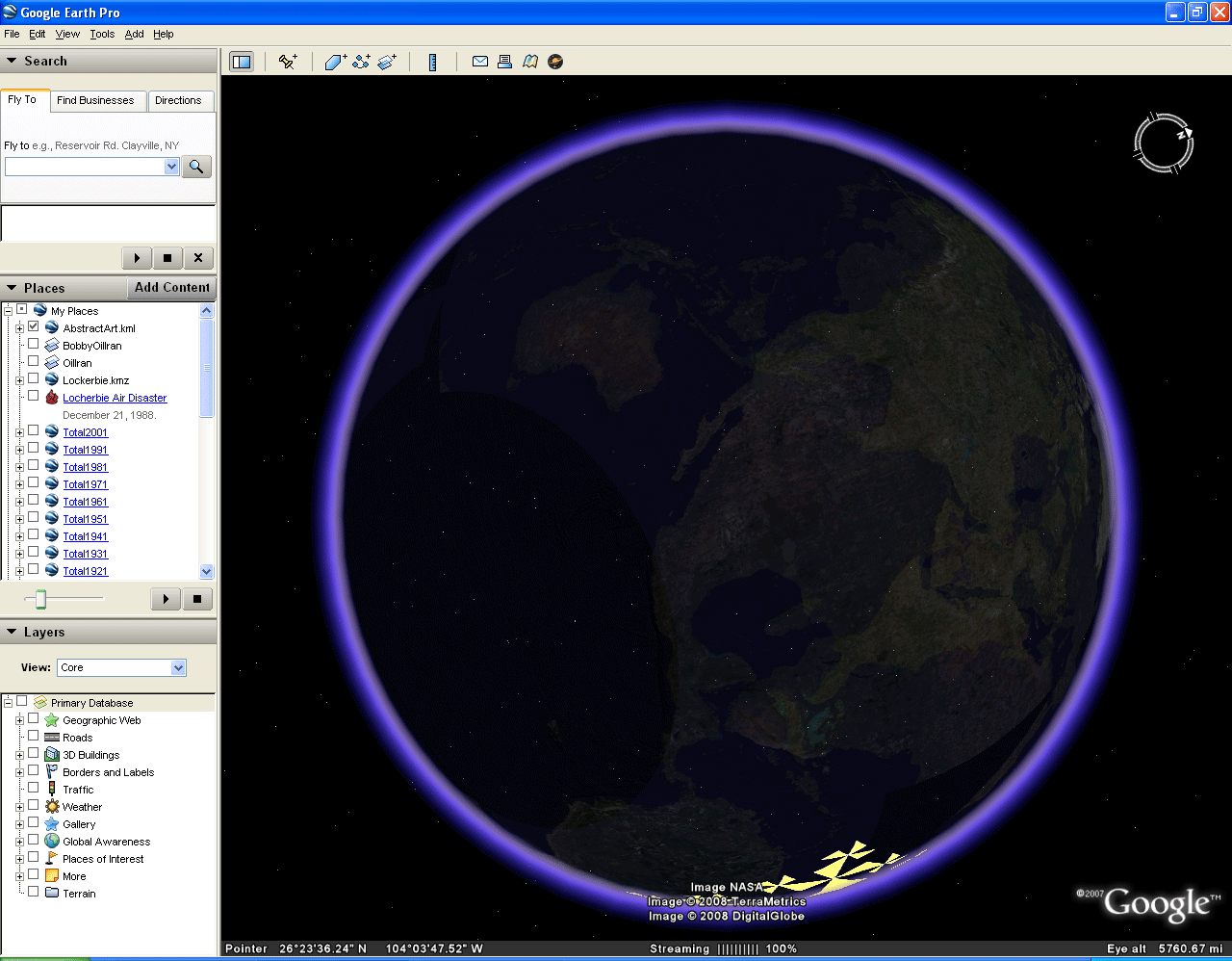Figure 4.  Transparency of the Pattern:  Eclipsing the Google Globe.


DAVID BARR'S FOUR CORNERS SCULPTURE
     One application that benefits greatly from the transparent globe effect is the visualization of David Barr's Four Corners Sculpture.  In the late 20th century, Barr set out to build an Earth-sized sculpture composed of actual small pyramids representing the vertices of an abstract tetrahedron inscribed in the earth-sphere.  More than a mere exercise, Barr actually travelled to four remote locations and planted the corners.  He began in Easter Island, continued to the Kalahari Desert in southern Africa, went to the Greenland icecap, and ended up on a small island just off New Guinea.  His adventure, which took many years, is chronicled in a variety of places including in film shot by a crew from the Archives of American Art (Smithsonian Institution) that traveled with him. 

Today, it is an easy matter to use placemarks in Google Earth to located the positions where the Corners are on the Earth.   While the "placemark" feature in Google Earth was used to pinpoint location by typing in exact latitude and longitude, polygons small enough not to experience any substantial eclipsing effect (as above) were also created at each Corner location.  The reason for doing so is that placemarks do not show up on the back side of the globe when it is made to be transparent; added polygons do show. 

One evident advantage to using Google Earth is that the reader can zoom in and get some modest appreciation for the surrounding terrain and the degree of difficulty the artist must have encountered in placing the vertices in disparate locations.  Download the associated .kml file to do so.  Figure 5 (a through d) shows a sequence of screen captures from the .kml file associated with each of the Four Corners. 


Figure 5a.  Barr and team began in Easter Island.  They had surveying equipment of Thor Heyerdahl.  There, the first movement of the Four Corners Ballet was danced by, among others, Barr's wife Beth.

Figure 5b.  The second vertex was planted on a farm, called "Karee Boom" in southern Africa.  There the second ballet movement was danced as the vertex was planted.  The ceremony was attended peacefully by both white and black Africans.

Figure 5c.  The third vertex was planted on the Greenland icecap.  As Barr left the site, a vicious storm formed around his tiny plane forcing him to jettison most of his equipment in order to survive.

Figure 5d.  Despite the adversity encountered elsewhere, the New Guinea vertex proved, in the end, the most difficult.  Repressive political problems forced  interminable delays and eventually only an agreement to move the calculated location from the main island to a tiny island got Barr the permission he needed to finish his sculpture.


     One problem with visualizing this scupture is that all four vertices are not simultaneously visible.  The traveler on the surface of the Earth has only views such as those in Figure 5.  An air traveller might get a glimpse of at most two of the vertices (or markers representing them) on the horizon of the hemisphere. Because the Corners are placed all around the sphere, it is not possible to see both front and back at the same time.  Or, is it?  When the sphere is made transparent, as in Figure 6, then all four vertices can be seen simultaneously!  Rotating the Google globe produces different patterns of where the vertices are in relation to the horizon surrounding the hemisphere. 


Figure 6.   Download the associated .kml file.

Drawing a path joining vertices (Figure 7), as a graph with edges lying along arcs of great circles on the transparent globe, clearly reveals the entire tetrahedral pattern.  It is only with transparency that such pattern becomes clear.

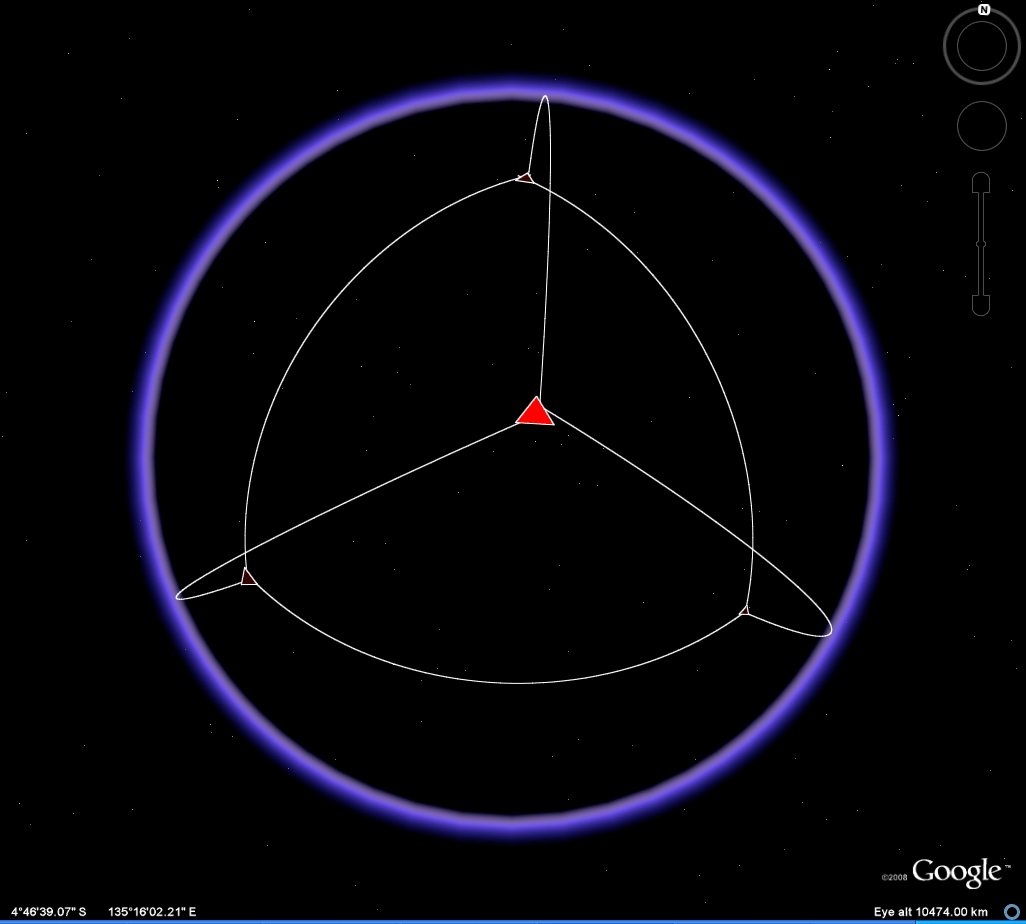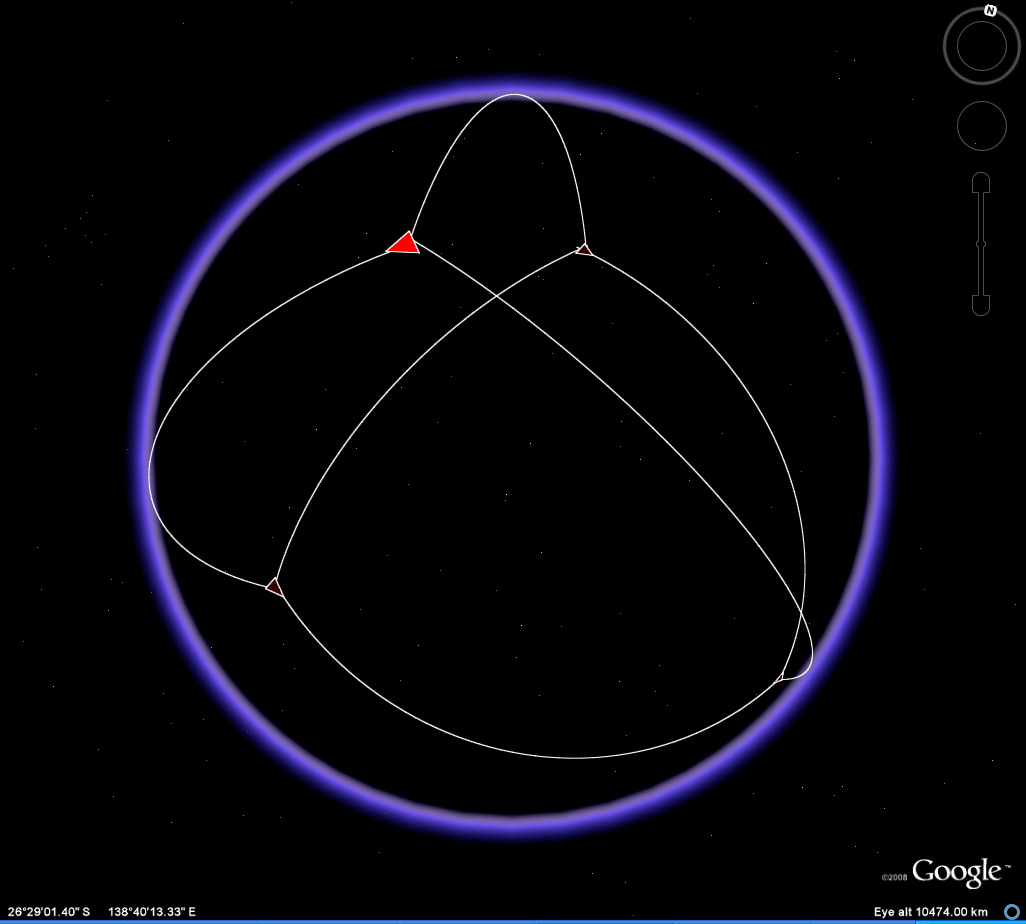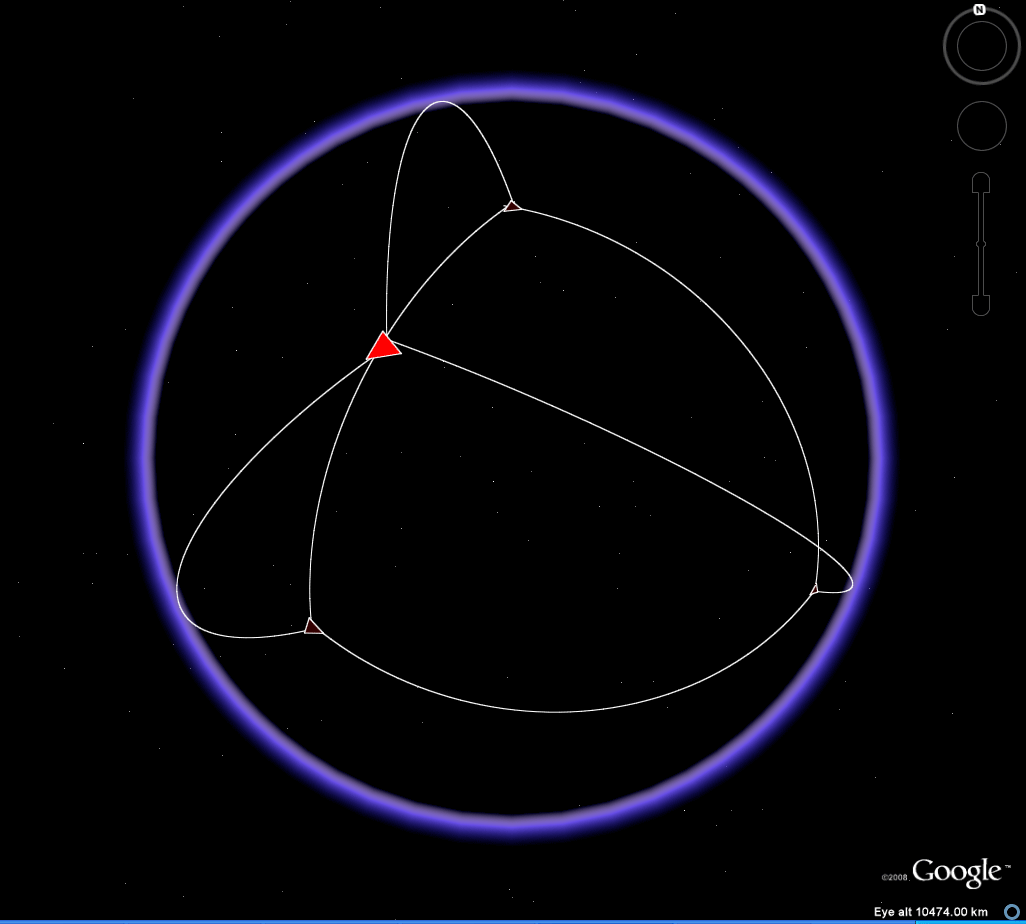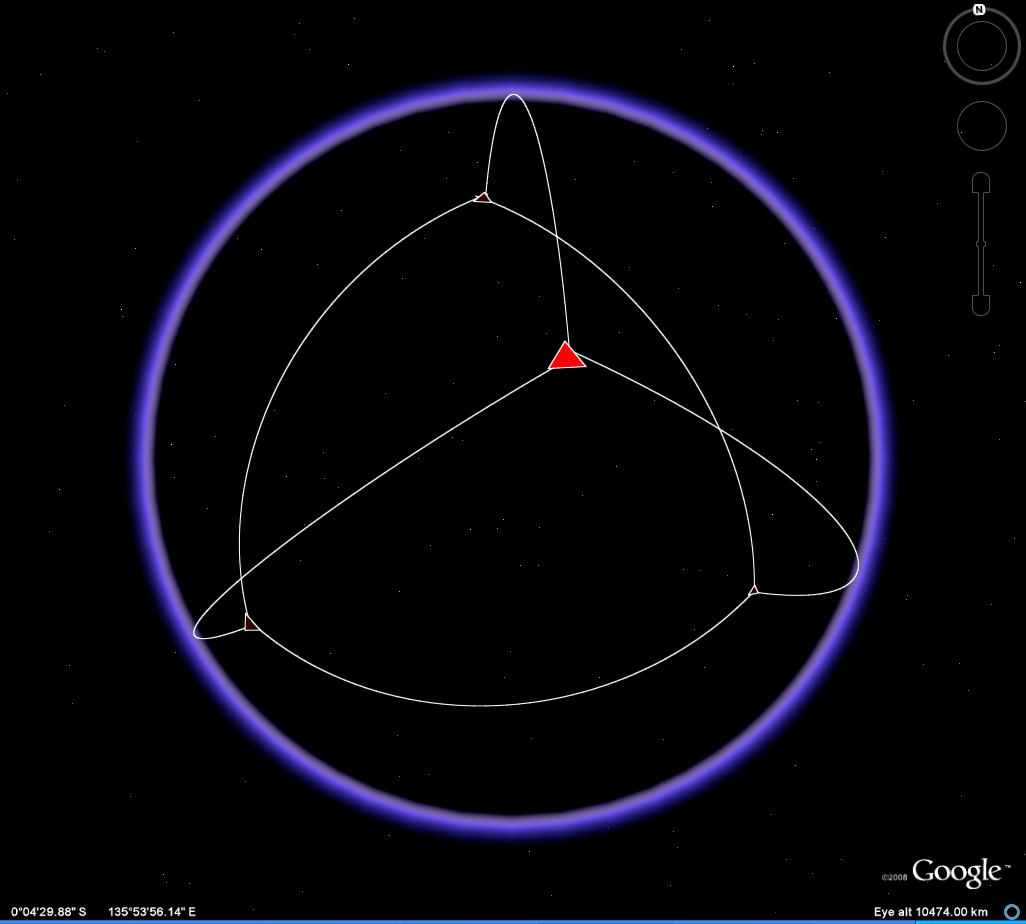Figure 7.   The associated .kml file is contained within the download for Figure 6.

Combining the various effects from above, in a linked movie file, produces a visual summary and demonstrates the necessity of transparency in visualizing the whole as the sum of its parts for this sculpture.


Science or demography applications of the transparency and eclipsing effects to come.  Compare and contrast "self-eclipsing" with "self-similarity" and develop a parallel to "fractal."


REFERENCES: 


Dr. Arlinghaus is Adjunct Professor at The University of Michigan, Director of IMaGe, and Executive Member, Community Systems Foundation.

Solstice:  An Electronic Journal of Geography and Mathematics, Institute of Mathematical Geography, Ann Arbor, Michigan.
Volume XIX, Number 2.
http://www.InstituteOfMathematicalGeography.org/
Persistent URL:  http://deepblue.lib.umich.edu/handle/2027.42/58219